Il y a 10590 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
Fiche Exercices passage à l’unité et proportionnalité
Télécharge la fiche d’exercices sur la proportionnalité et le passage à l’unité CM2 CM1
DESCRIPTION
Proportionnalité et passage à l’unité
Cette vidéo pour les élèves de cycle 3 (CM1, CM2, 6ème) a pour objectif d’apprendre à résoudre des problèmes relevant de la proportionnalité en passant par l’unité. Face à une situation de proportionnalité et quand c’est pertinent, le passage à l’unité est une bonne manière de résoudre un problème. Pour cela, il faut que l’unité soit facile à trouver à l’aide d’une division ou d’une multiplication.
J’aborde également les tableaux de proportionnalité afin que les élèves rencontrent des représentations différentes et puissent l’utiliser pour visualiser facilement le passage à l’unité.
LE CONSEIL DE MAITRE LUCAS
Exemple de la vie courante
Dans ce chapitre sur la proportionnalité, il est toujours important de donner du sens aux apprentissages en faisant des liens avec la vie quotidienne.
Il y a plusieurs méthodes pour résoudre un problème de proportionnalité, il est alors important de laisser votre enfant chercher une solution qui lui convienne avant d’en montrer d’autres.
Compétences acquises
- Reconnaître et résoudre des problèmes relevant de la proportionnalité en utilisant une procédure adaptée : passage à l’unité.
- Identifier une situation de proportionnalité entre deux grandeurs à partir du sens de la situation.
- Résoudre un problème de proportionnalité impliquant des grandeurs.
À qui s’adresse cette vidéo ?
Niveau
CM1 (Cours Moyen 1ère année)
CM2 (Cours Moyen 2ème année)
Matière
Mathématiques, Maths
Cours
Grandeurs et mesure, la proportionnalité
Proportionnalité et passage à l’unité
Hey salut ! On se retrouve pour la seconde vidéo sur la proportionnalité. Dans la vidéo précédente, nous avions vu ce qu’est une situation de proportionnalité et comment résoudre certains problèmes en utilisant les additions et les multiplications. Maintenant, on va utiliser le passage à l’unité, c’est parti !

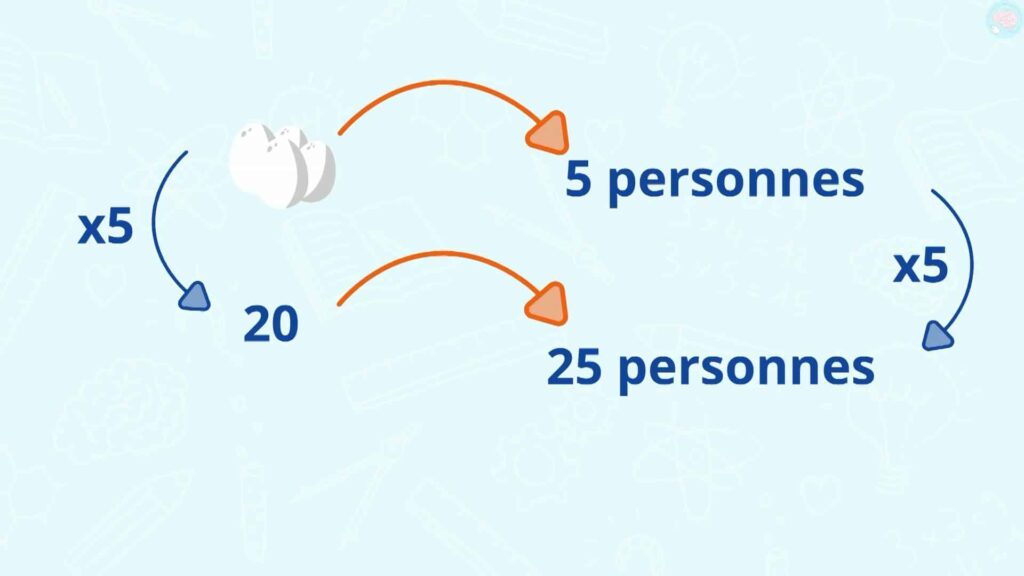
Je reprends rapidement un de nos problèmes. Pour faire des crêpes, on avait besoin de 4 œufs pour 5 personnes et nous étions 25. On a fait 5 + 5 + 5 + 5 + 5 pour tomber sur 25 et l’on a donc fait la même chose avec 4 + 4 + 4 + 4 + 4 et l’on a trouvé 20 œufs. Ça, c’est une méthode avec l’addition.
On pouvait faire la même chose avec une multiplication si l’on connaît bien ces tables, on sait que 5 x 5 ça fait 25, alors je fais juste 4 x 5 et je trouve 20. C’est la méthode avec la multiplication.
Problème de proportionnalité et de passage à l’unité
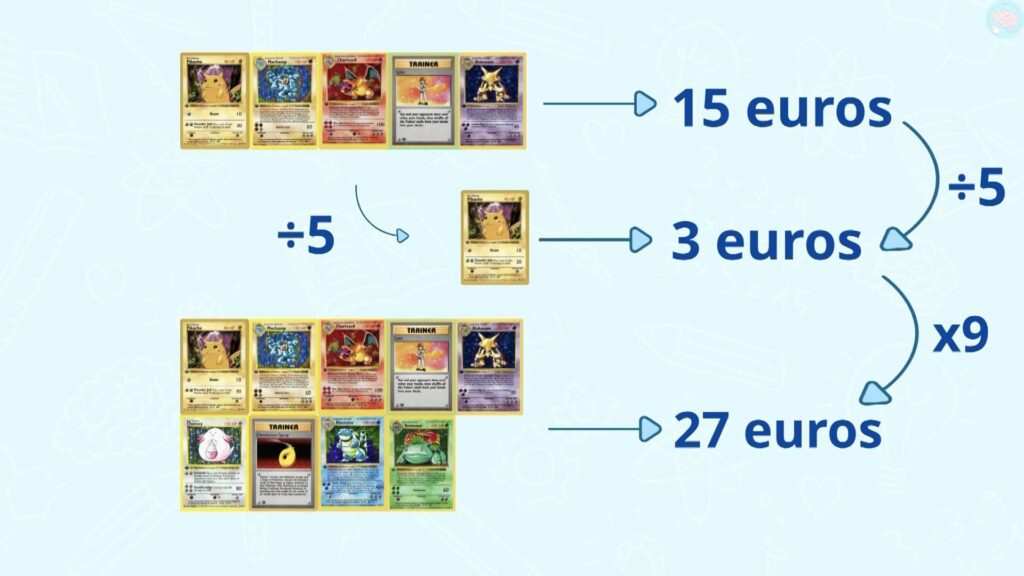
Maintenant, je vais te mettre un nouveau problème à résoudre et tu vas essayer d’y réfléchir. 5 cartes Pokémon coûtent 15 euros, combien coûtent 9 cartes Pokémon ? Cherche une ardoise ou une feuille et mets pause pour y réfléchir.
Je peux participer ? Évidemment, comment ferais-tu ? Ben, mon problème c’est que si je fais 5 cartes + 5 cartes, je tombe sur 10 et pas sur 9. Donc la méthode des additions ne fonctionne pas. Et 9, ce n’est pas dans la table de 5, donc la méthode de la multiplication ne fonctionne pas non plus. Effectivement, il faut trouver une autre technique. Si je connaissais le prix d’une seule carte, ce serait plus simple, je pourrais facilement trouver combien coûtent 9 cartes. Eh bien justement, est-ce que tu es sûr que tu ne connais pas le prix d’une seule carte ? Si 5 cartes coûtent 15 euros…
Pour passer de 5 cartes à 1 carte, je divise par 5. Alors si je fais 15/5 aussi, ça fait 3, 3 euros. Eh bien voilà, le prix d’une carte est de 3 euros. Tu as divisé les cartes et les euros par le même nombre et tu as trouvé le prix d’une seule carte. Et maintenant facile, je fais 3 x 9, ça fait 27 euros. Exactement.
La méthode de l’unité
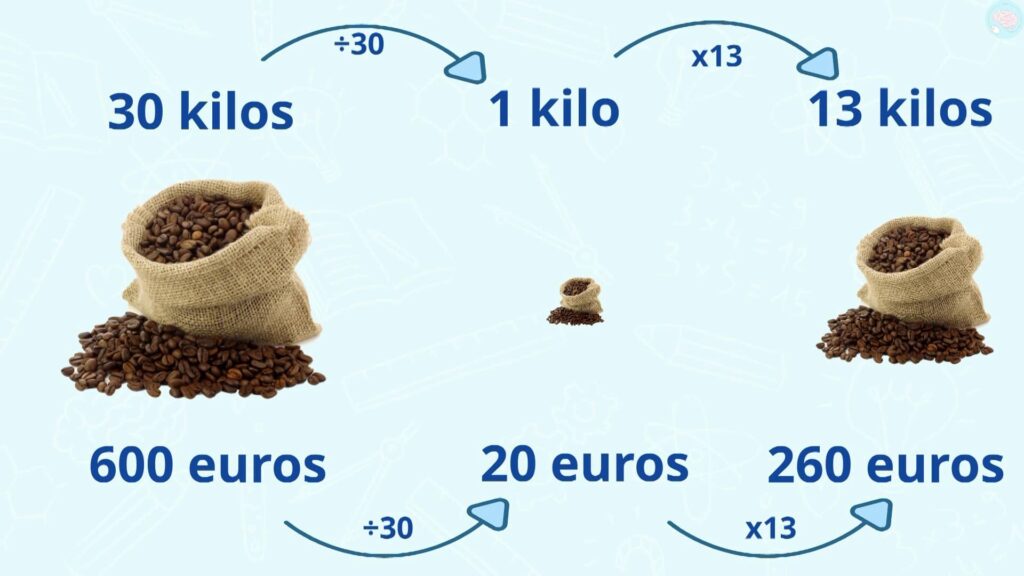
Dans certaines situations, tu as besoin de cette méthode. Tu cherches alors combien vaut 1, une unité, tu passes par l’unité. Un autre exemple, 30 kg de café coûtent 600 euros, combien coûtent 13 kg ? Toi derrière ton écran, est-ce que tu peux me trouver la réponse ? Mets pause.
En utilisant la technique du passage par l’unité, il faut que tu trouves le prix d’un kilo, alors tu fais 30 kg/30, ça fait 1, et 600/30, ça fait 20, donc 1 kilo, c’est 20 euros.
Maintenant que tu as le prix de 1 kg, d’une unité, il te suffit de multiplier par 13 pour trouver 13 kg. Donc 1 kg x 13, ça fait 13 kg et 20 € x 13, ça fait 260 €. 13 kg de café coûtent de 260 euros.
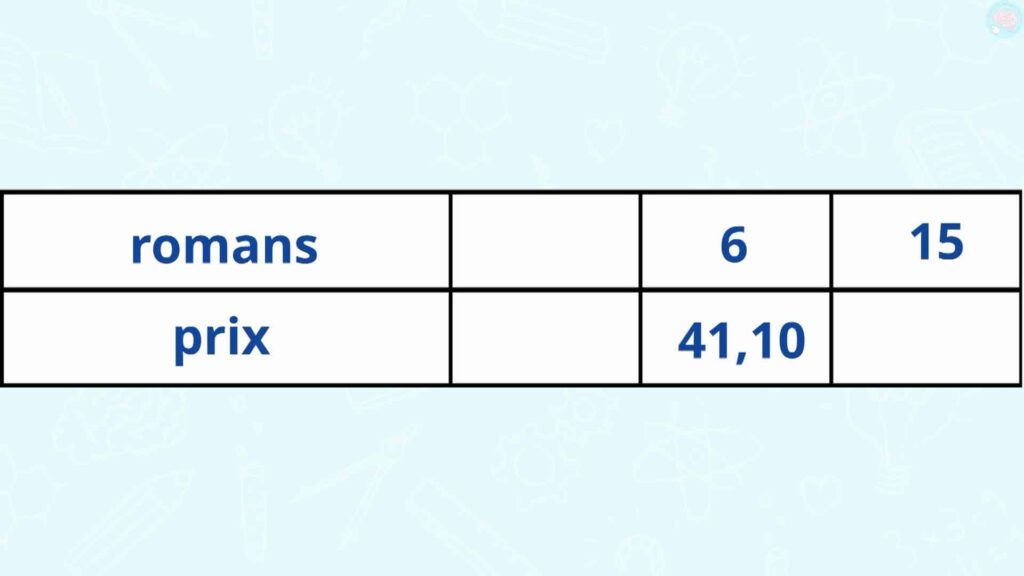
Tableau de proportionnalité et passage à l’unité
Un autre exemple, j’achète 6 romans, ils ont tous le même prix et en tout ils écoutent 41,10 euros, combien vont coûter 15 romans ? Mets pause, donne-moi la réponse.
Je crois que j’ai trouvé quelque chose. Comme avant je divise par 6, pour trouver le prix d’un romain. Donc je fais 6/6 et 41,1/6. Oh là là, je ne peux pas faire ça de tête.
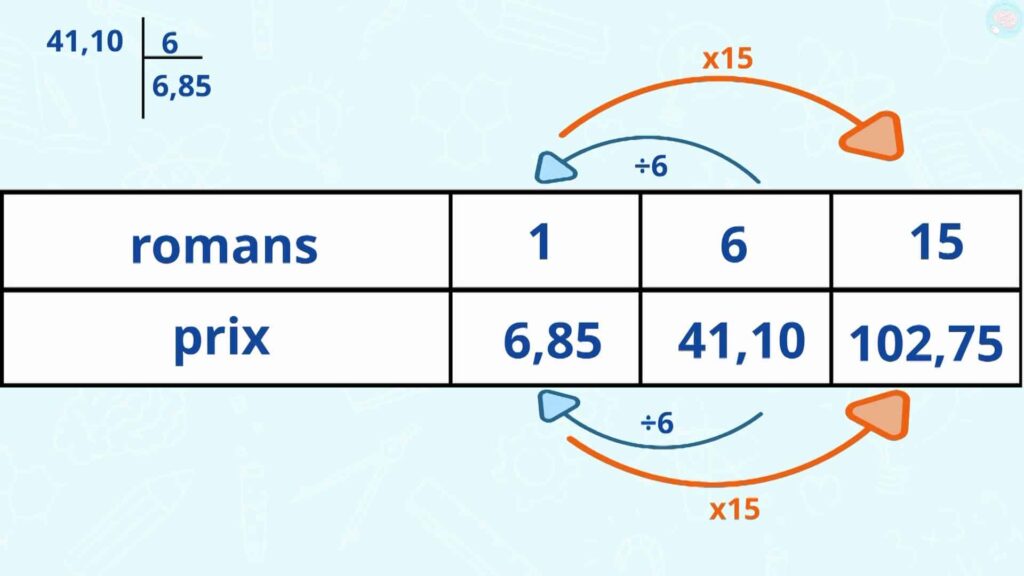
Attends, je le pose vite fait. Et voilà, ça fait 6,85. Après je multiplie par 15 et je trouve 102,75 euros. Donc 15 romans vont coûter 102,75 €. Exactement.
Exemple
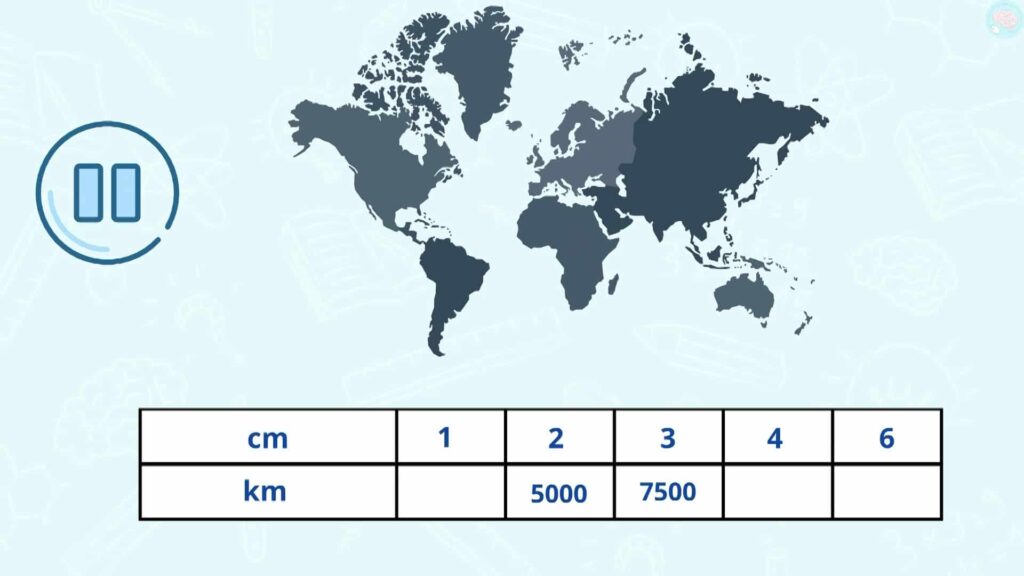
Maintenant, regarde cette carte, en dessous, j’ai mis un tableau dans lequel, il y a ce que l’on appelle une échelle. 1 cm sur la carte, on ne sait pas à quoi ça correspond dans la réalité. Mais on sait que 2 centimètres sur la carte, c’est 5000 km dans la réalité. 3 cm, c’est 7500 km, 4 cm on ne sait pas et 6 cm non plus. Pour remplir ce tableau, tu peux utiliser les techniques que l’on a vues ensemble, notamment le passage par l’unité. Mets pause et prends le temps de le remplir sur une ardoise ou une feuille.
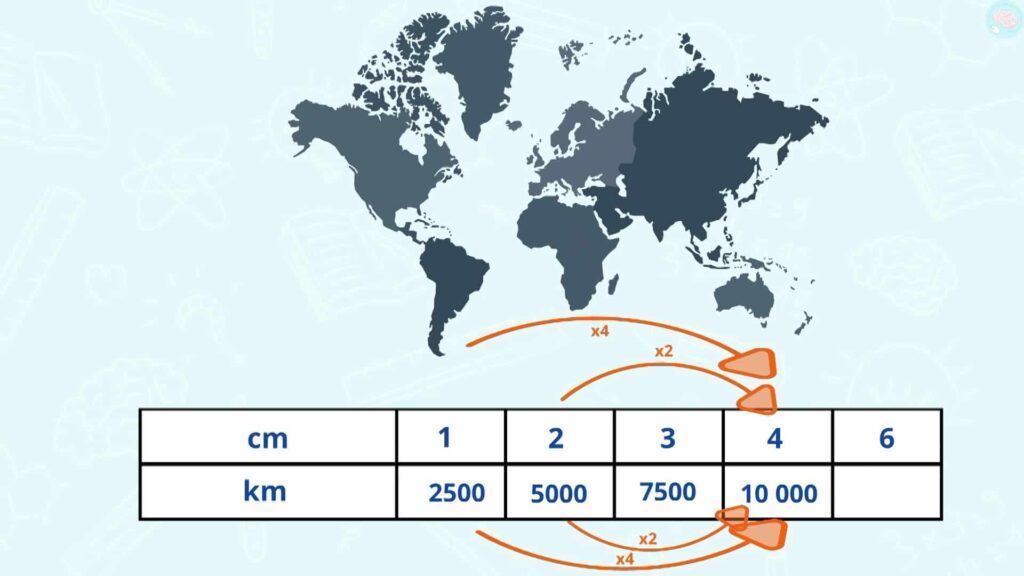
C’est bon, tu as tout trouvé ? Je corrige. Pour trouver à quoi correspond 1 cm, je fais 2/2 pour trouver 1, donc 5 000/2 = 2 500. Donc 1 cm sur la carte correspond à 2 500 km dans la réalité.
Pour trouver 4 cm, tu pouvais faire 1 x 4 et 2 500 x 4, ou alors 2 x 2 et 5000 x 2, dans les deux cas, tu trouves 10 000 km.
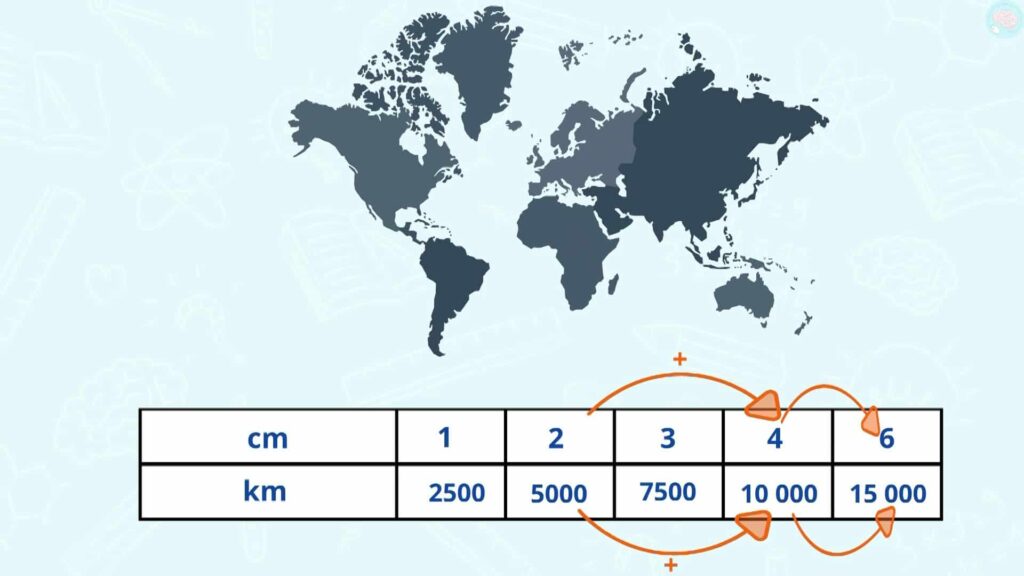
Et pour trouver 6 cm, tu as plusieurs techniques. Tu peux faire 1 x 6, 2 x 3, 3 x 2. Tu trouves dans tous les cas 15 000, et tu pouvais aussi très bien faire, 2 + 4, ça fait 6. Donc 5 000 + 10 000, ça fait aussi 15 000.
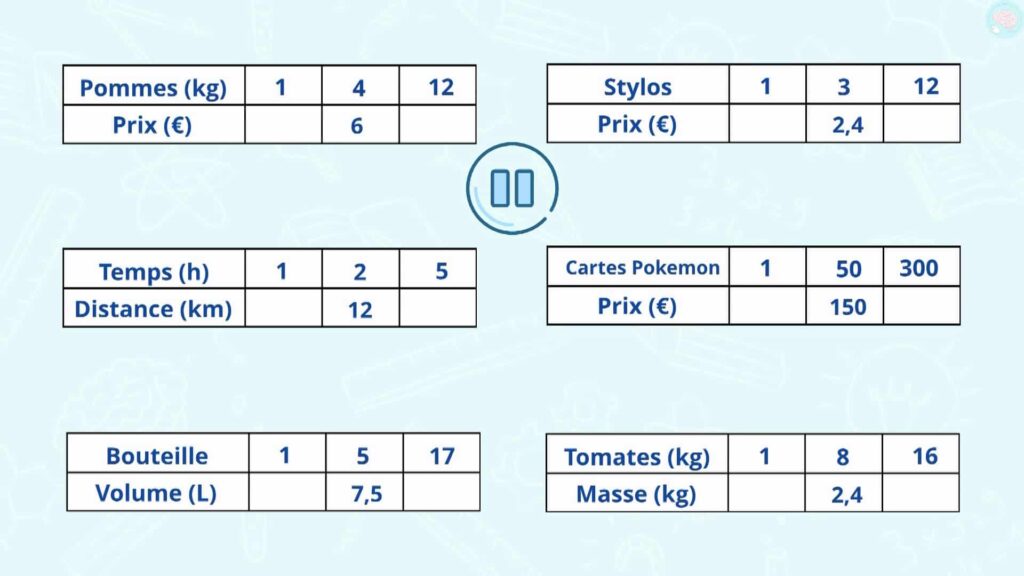
Exercices proportionnalité et passage à l’unité
Je te propose maintenant plusieurs tableaux à compléter, essaie de les compléter en passant par l’unité. Mets pause, c’est parti.
Réponse
Je commence par faire une division pour trouver l’unité dans chaque tableau. Regarde bien. Ensuite, il me suffit de faire une multiplication pour compléter le tableau en entier. Et voilà, compare avec ce que tu avais trouvé.
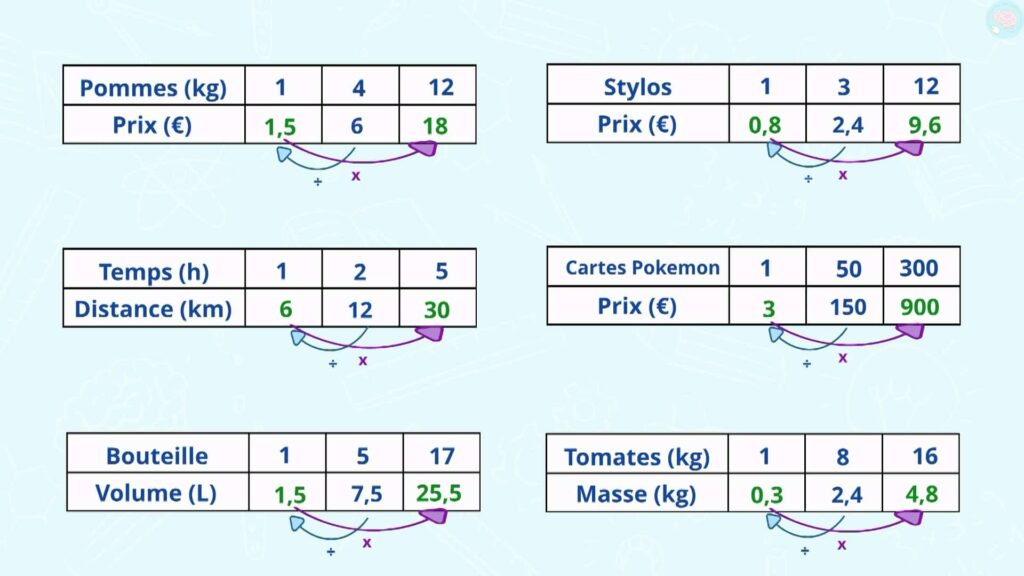

Dans cette vidéo, nous avons appris à résoudre des problèmes dans des situations de proportionnalité en passant par l’unité. Tu peux continuer à t’entrainer avec cette fiche, qui est sur maitrelucas.fr sous cette vidéo. On se retrouve très très bientôt. Salut.






4 réponses sur « La proportionnalité et passage à l’unité »
merci
Merci de m’avoir aidé
Vraiment bien expliqué ! bravo ! merci mille fois
Merci beaucoup