Il y a 9542 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
Fiche d’exercices
Télécharge la fiche d’exercices pour t’entrainer :
DESCRIPTION
Soustractions posées sans retenue
Cette vidéo a pour but d’apprendre à poser les soustractions sans retenue. Elle est destinée aux élèves de CE1 et CE2. J’amène les élèves à comprendre comment poser une soustraction sans retenue. Tout part d’une petite situation concrète : un puzzle de 958 pièces dont 432 sont déjà assemblées. L’objectif est simple, mais il pousse à se demander combien il reste à poser. À partir de là, les enfants découvrent que la soustraction permet justement de trouver ce qui manque pour compléter un tout.
Je montre ensuite, pas à pas, comment poser le calcul. On dispose les nombres l’un sous l’autre, en alignant bien les unités, les dizaines et les centaines, puis on soustrait colonne par colonne. Le calcul se fait toujours du côté des unités, avant de passer aux dizaines et aux centaines. Grâce à cette méthode, les élèves voient qu’il suffit d’être attentif au placement des chiffres pour éviter les erreurs.
L’idée est aussi de montrer que cette technique fonctionne pour n’importe quel nombre, petit ou grand. Les enfants s’exercent avec des exemples variés et comprennent que la soustraction posée n’est pas un nouveau calcul, mais une manière organisée de raisonner. En s’entraînant régulièrement, ils prennent confiance et gagnent en autonomie face à des nombres plus complexes.
Cette vidéo permet de consolider les bases du calcul posé tout en préparant la suite : les soustractions avec retenue.
LE CONSEIL DE MAITRE LUCAS
Lier cela à la résolution d’un problème
Vous pouvez donner à votre enfant des occasions de les relier à des situations concrètes. Par exemple, lorsqu’il range ses jouets ou prépare la table, vous pouvez lui demander combien d’objets il reste après en avoir retiré quelques-uns. Ces petits moments du quotidien l’aident à comprendre que la soustraction sert avant tout à mesurer une différence ou à calculer ce qu’il reste.
Il est souvent utile de le laisser manipuler. Avec des jetons, des pièces ou des bonbons, il peut matérialiser les unités, former des paquets de dix et constater ce qui se passe lorsqu’on en enlève une partie. Ce passage par le concret rend les calculs posés beaucoup plus clairs lorsqu’il passe ensuite à l’écrit.
Lorsque votre enfant pose une soustraction, encouragez-le à bien observer la disposition des chiffres. Un simple décalage peut tout changer, et c’est souvent en repérant lui-même ses erreurs qu’il progresse le plus. Plutôt que de corriger immédiatement, invitez-le à vérifier en relisant ou en recomptant : “Es-tu sûr que les unités sont bien sous les unités ?” ou “Regarde, ton résultat te semble logique ?”. Ces petites questions l’amènent à réfléchir à sa démarche.
Enfin, rappelez-lui que la rigueur s’acquiert avec la pratique. Même si les premières soustractions paraissent longues, chaque essai le rend plus à l’aise. L’important n’est pas d’aller vite, mais de comprendre ce que l’on fait. Avec le temps, poser une soustraction deviendra pour lui aussi naturel que faire une addition.
Compétences acquises
- Poser une soustraction en alignant correctement les chiffres selon leur position.
- Calculer une soustraction sans retenue en procédant colonne par colonne.
- Vérifier le résultat d’une soustraction en reliant le calcul à une situation concrète.
À qui s’adresse cette vidéo ?
Niveau
CE1 (Cours élémentaire 1ère année)
CE2 (Cours élémentaire 2ème année)
Matière
Maths, Mathématiques
Cours
Nombres et calculs
Résoudre un problème par la soustraction posée sans retenue
Hey mon garçon ! Tu as vu mon puzzle de 958 pièces, j’ai bientôt terminé. Tu en as posé combien ? J’en ai posé exactement 432. Euh, il faut en poser combien encore ? Eh bien, à toi de me dire. Euh attends… 958… Maître Lucas !!! Oui, oui, je suis là, qui y a-t-il ? Papi a 1 puzzle de 958 pièces et il a déjà posé 432, il faut que je trouve combien de pièces il lui reste à poser.


Additions posées sans retenue
Est-ce que tu sais quelle opération tu vas devoir utiliser ? Je sais qu’il faut que je cherche la différence entre les pièces qu’il a déjà posées et celles qui restent. Je dirais alors un « — » une soustraction. Exactement, et pour cela, on peut utiliser la technique des soustractions posées sans retenue. On va la voir tout de suite.
Quand tu es face à une grosse soustraction que tu ne peux pas résoudre de tête, tu peux la poser. Eh, mais comme les additions posées ? Tout à fait, c’est un peu la même chose.
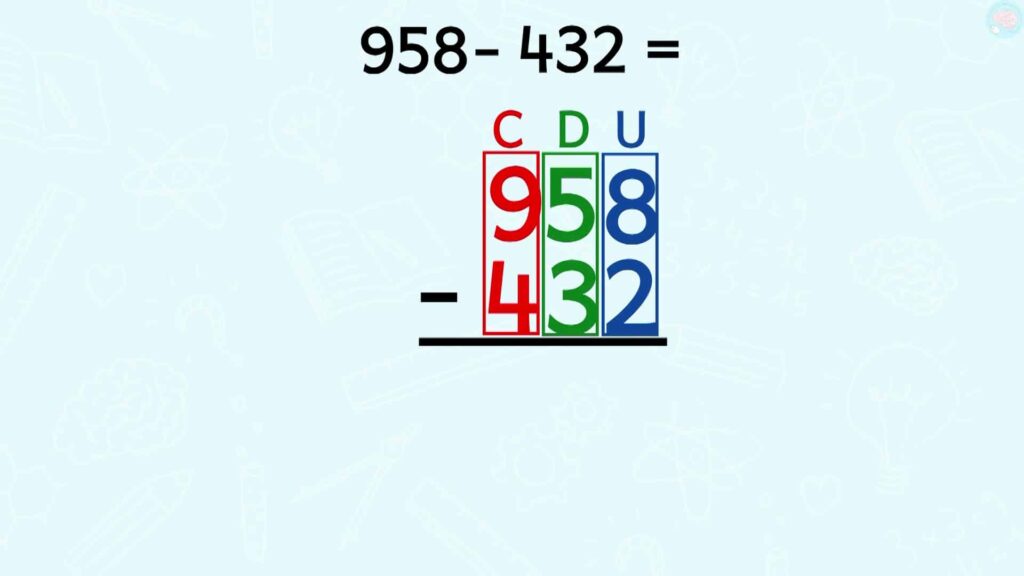
Comment poser une soustraction ?
Comme pour les additions posées, tu mets bien les chiffres des unités sous les unités, les chiffres des dizaines sous les dizaines et les chiffres des centaines sous les centaines. Tu mets le nombre le plus grand au-dessus.
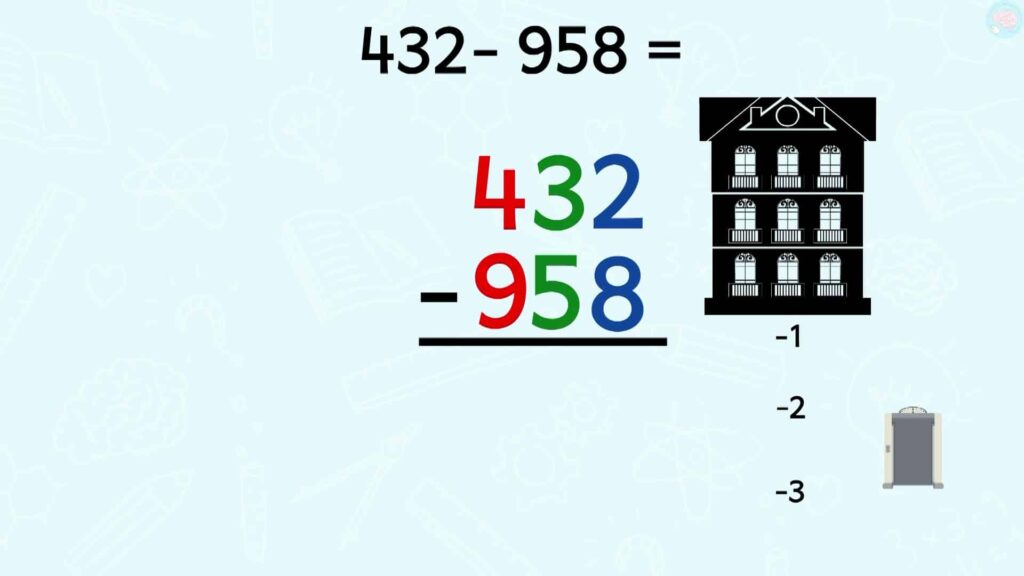
Ben oui, on ne peut pas enlever 958 à 432. Là, pour toi, ce n’est pas possible, mais on pourrait avec les nombres négatifs comme un ascenseur quand il descend à -1 – 2 -3, mais ça, on ne le verra pas tout de suite. Je vais démarrer la soustraction et tu pourras suivre avec les cubes juste à côté.
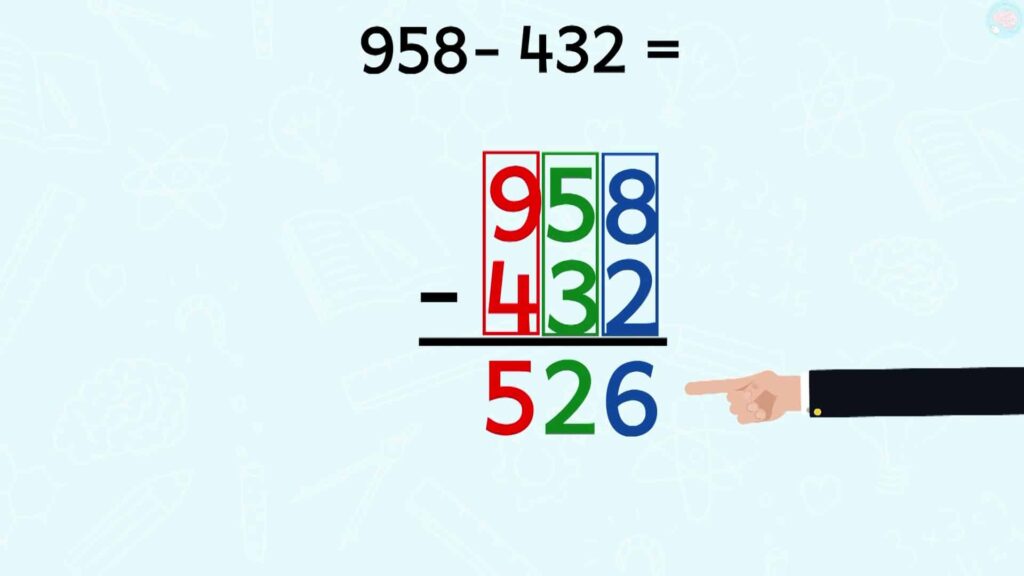
Quand ta soustraction est bien posée et que les chiffres sont bien alignés, tu commences par les unités comme pour les additions. Je fais donc 8 – 2, ça fait combien ? 6 6 6 Oui oui, ça fait 6, je note 6. Ensuite 5 – 3, ça fait 2 et 9 – 4 ça fait 5. Le résultat est 526.
Ces soustractions sans retenu, je pourrais même les faire de tête en faisant du calcul en ligne. Regarde, si je commence par les unités, je fais 8 – 2, j’écris 6, 5 – 3, j’écris 2 et 9 – 4, j’écris 5. Et voilà, j’ai déjà le résultat 526. Je n’ai même pas eu besoin de poser le calcul. Eh papi ! Il te reste 526 pièces de puzzle à poser. Tu n’as pas du tout terminé. Oh zut alors Jacqueline, viens m’aider.

Faire le calcul avec une soustraction posée sans retenue
Donc je répète, tu poses ta soustraction en mettant bien les chiffres des unités sous les unités, les chiffres des dizaines sous les dizaines et les chiffres des centaines sous les centaines, et cetera si le nombre est plus grand.
Ensuite, tu fais les soustractions en commençant par les unités et voilà, c’est tout. Avec cette technique, tu peux résoudre plein de problèmes que tu ne peux pas faire de tête.

Exercices soustractions posées sans retenue
Pour que tout ceci reste bien dans ta tête, il faut s’entraîner. Voici des soustractions à faire pour toi qui est derrière ton écran. Prends une ardoise ou une feuille et tu peux toutes les faire. Attention à bien aligner les chiffres. Mets pause, c’est parti.
Réponse

Et je corrige avec la première soustraction 784 – 261. Je commence bien sûr par les unités. 4 – 1 ça fait 3. Ensuite 8 – 6, ça fait 2. Et 7 – 2, ça fait 5. 523. Puis je continue. Je commence par les unités. 3 – 2 ça fait 1. 5 – 4 ça fait 1 et 5 – 0, puisque je n’ai rien ici, ça fait 5. Résultat 511. Puis 6 – 3 ça fait 3, 6 – 6 ça fait 0 et 4 – 2 ça fait 2. Donc 203. Je continue. 4 – 1 ça fait 3. 8 – 6 ça fait 2. Résultat 23. Pour les calculs où il n’y a plus les couleurs, 3 – 2 ça fait 1, 5 – 4 ça fait 1, 2 – 1, ça fait 1. Résultat 111. Calcul suivant : 6 – 4 ça fait 2. 7 – 3 ça fait 4 et 8 – 2, ça fait 6, résultat 642. Et enfin 9 – 2, ça fait 7, 6 – 1, ça fait 5 et 5 – 3, ça fait 2. Résultat 257. Tu peux maintenant comparer ces résultats avec ce que toi tu as écrit. Et si tu as des erreurs, tu cherches d’où viennent tes erreurs. Comme ça, elles te permettent d’apprendre. Mets pause.

Maintenant, je te propose de faire ces trois soustractions, mais elles ne sont pas posées. Alors, à toi de les poser, mets pause.
Réponse

Évidemment, lorsque l’on pose des calculs, il faut bien aligner les chiffres. Je commence par 675 – 541 et donc par les unités également. 5 – 1 ça fait 4. 7 – 4 ça fait 3 et 6 – 5 ça fait 1. Résultat 134. Puis, calcul suivant 6 – 1, ça fait 5. 7 – 2 ça fait 5 aussi et 9 – 3 ça fait 6. Résultat 655. Et pour le dernier 8 – 2, ça fait 6. 4 – 3 ça fait 1 et 5 – 2 ça fait 3. Résultat 316. Mets pause et compare avec ce que toi tu as écrit.

Outro et fiche d’exercices Soustractions posées sans retenue
Dans cette vidéo, tu as découvert les soustractions posées sans retenue, mais bientôt, nous parlerons des soustractions posées avec retenue. En attendant, tu peux t’entraîner avec cette fiche qui est sur le site maitrelucas.fr sous cette vidéo. À plus !




3 réponses sur « Soustractions posées sans retenue »
Bonjour,
Merci pour vos articles, leçons, fiches, exercices, .. : c’est clair, bien expliqué.
Je me permets de corriger :
“Faire le calcul avec une soustractions posées sans retenues” : merci de retirer les s à soustractions posées puisqu’il n’y en a qu’une.. !
Bonjour, merci pour votre vigilance. J’ai corrigé l’erreur.
Maître Lucas
Et ge ne savai pas tout sa wow