Il y a 4603 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
Fiche d’exercices
Télécharge la fiche d’exercices pour t’entrainer :
DESCRIPTION
Soustractions posées sans retenue
Cette vidéo a pour but d’apprendre à poser les soustractions sans retenue. Elle est destinée aux élèves de CE1 et CE2. Il s’agit de comprendre que la soustraction est à poser uniquement dans certaines situations (1000-980 ou 100-18 n’en font pas partie par exemple). Les élèves doivent alors penser à bien aligner les unités, les dizaines, etc. Après avoir posé les nombres avec le plus grand au-dessus, ils calculent chaque soustraction en commençant par les unités.
LE CONSEIL DE MAITRE LUCAS
Lier cela à la résolution d’un problème
La soustraction posée n’est pas à utiliser quand les calculs sont faisables de tête. Elle doit également toujours avoir du sens et être liée à la résolution de problèmes.
Avant de proposer un calcul, n’hésitez pas à proposer un problème avec les nombres qui seront utilisés.
Compétences acquises
- Mettre en œuvre un algorithme de calcul posé pour la soustraction.
À qui s’adresse cette vidéo ?
Niveau
CE1 (Cours élémentaire 1ère année)
CE2 (Cours élémentaire 2ème année)
Matière
Maths, Mathématiques
Cours
Nombres et calculs
Résoudre un problème par la soustraction posée sans retenue
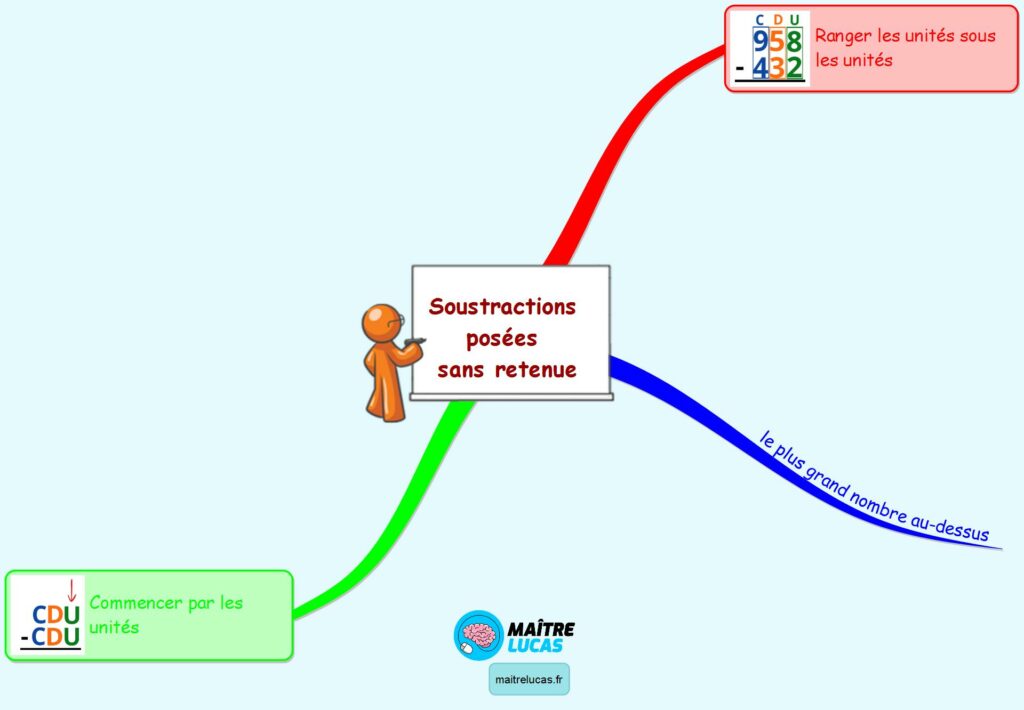
Hey mon garçon ! Tu as vu mon puzzle de 958 pièces, j’ai bientôt terminé. Tu en as posé combien ? J’en ai posé exactement 432. Euh, il faut en poser combien encore ? Eh bien, à toi de me dire. Euh attends… 958… Maître Lucas !!! Oui, oui, je suis là, qui y a-t-il ? Papi a 1 puzzle de 958 pièces et il a déjà posé 432, il faut que je trouve combien de pièces il lui reste à poser.


Soustractions posées sans retenue
Est-ce que tu sais quelle opération tu vas devoir utiliser ? Je sais qu’il faut que je cherche la différence entre les pièces qu’il a déjà posées et celles qui restent. Je dirais alors un « — » une soustraction. Exactement, et pour cela, on peut utiliser la technique des soustractions posées sans retenue. On va la voir tout de suite.
Quand tu es face à une grosse soustraction que tu ne peux pas résoudre de tête, tu peux la poser. Eh, mais comme les additions posées ? Tout à fait, c’est un peu la même chose.
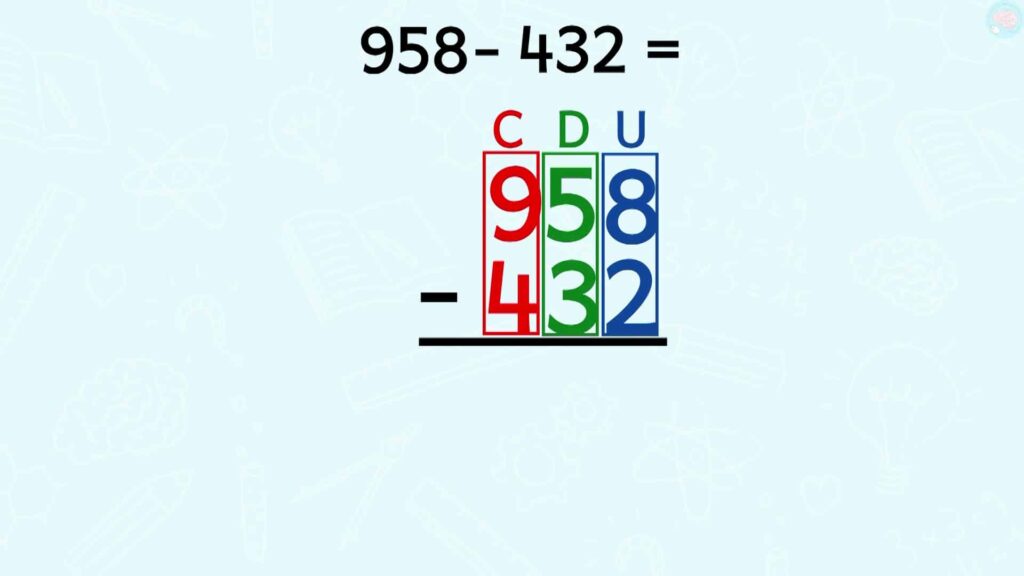
Comment poser une soustraction ?
Comme pour les additions posées, tu mets bien les unités sous les unités et les dizaines sous les dizaines et les centaines sous les centaines. Tu mets le plus grand nombre au-dessus.
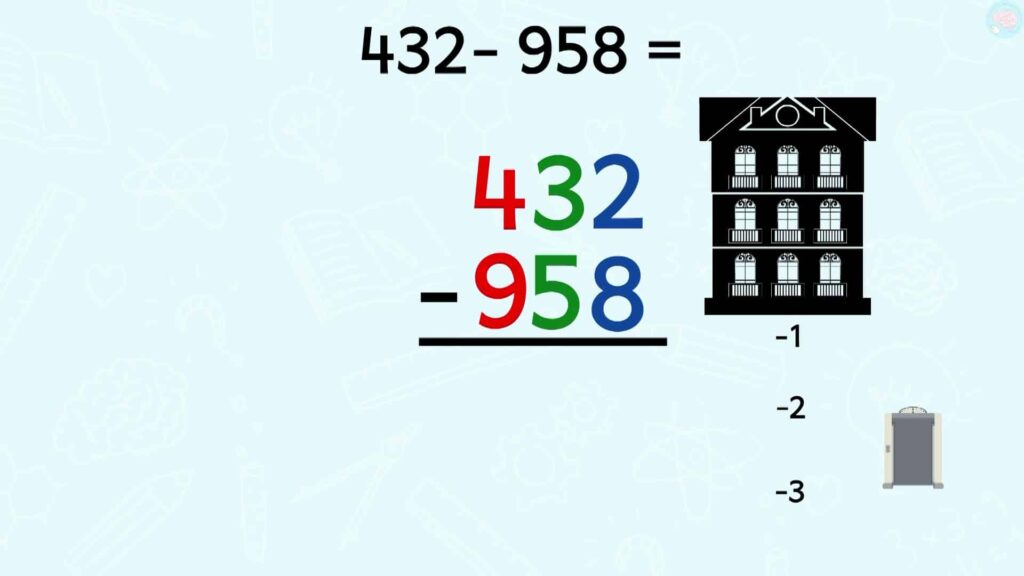
Ben oui, on ne peut pas enlever 958 à 432. Là pour toi ce n’est pas possible, mais tu pourrais si on rentre dans les nombres négatifs comme le fait un ascenseur par exemple, mais ça on ne le verra pas tout de suite.
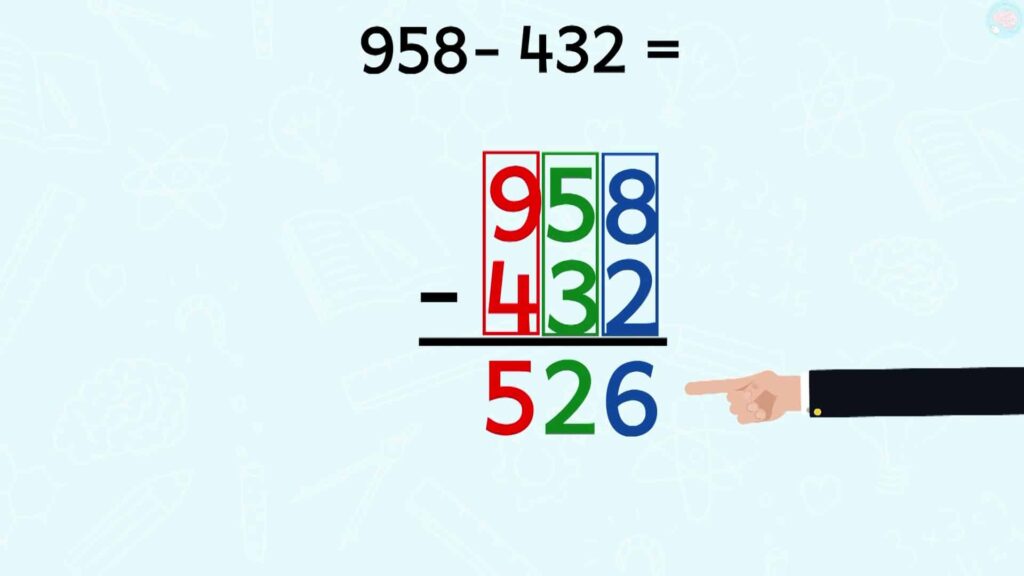
Quand ta soustraction est bien posée, tu commences par les unités comme pour les additions. Je fais donc 8 – 2, ça fait combien ? 6. Oui, oui, ça fait 6, je note 6. Ensuite, 5 – 3, ça fait 2, et 9 – 4, ça fait 5. Le résultat est 526.
Eh papi ! Il te reste 526 pièces du puzzle à poser, tu n’as pas du tout terminé. Oh zut alors ! Jacqueline vient m’aider.

Faire le calcul avec une soustraction posée sans retenue
Donc je répète, tu poses la soustraction en mettant bien les unités sous les unités, les dizaines sous les dizaines et les centaines sous les centaines, etc. si le nombre est plus grand.
Ensuite, tu fais les soustractions en commençant par les unités et voilà, c’est tout. Avec cette technique, tu peux résoudre plein de problèmes que tu ne peux pas faire de tête.
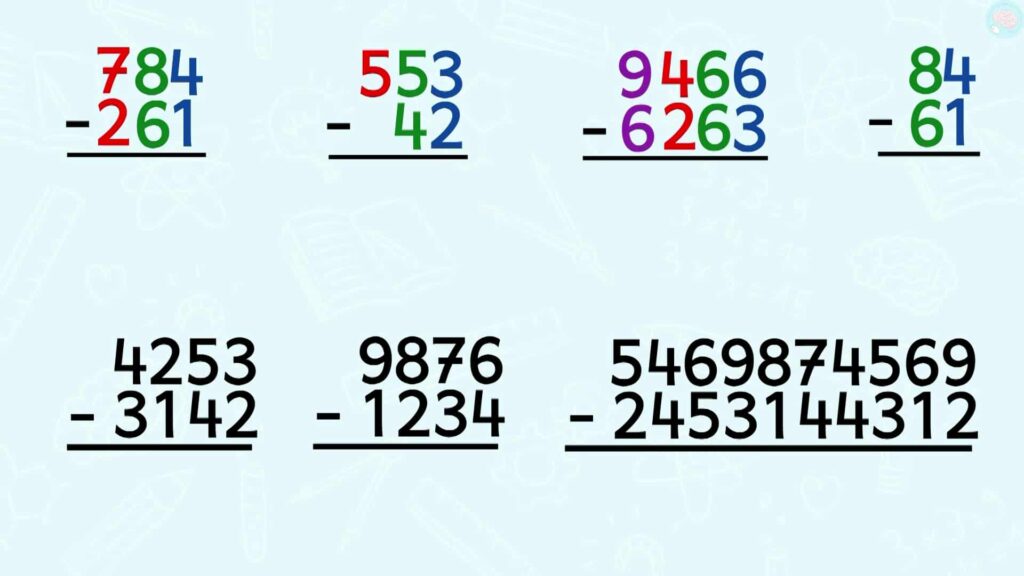
Exercices soustractions posées sans retenue
Pour que tout cela reste bien dans ta tête, il faut s’entrainer. Voici des soustractions à faire pour toi qui est derrière ton écran, prends une ardoise ou une feuille et tu peux toutes les faire. Attention, parfois j’ai mis de très grands nombres, mais la technique reste la même. Mets pause, c’est parti.
Réponse
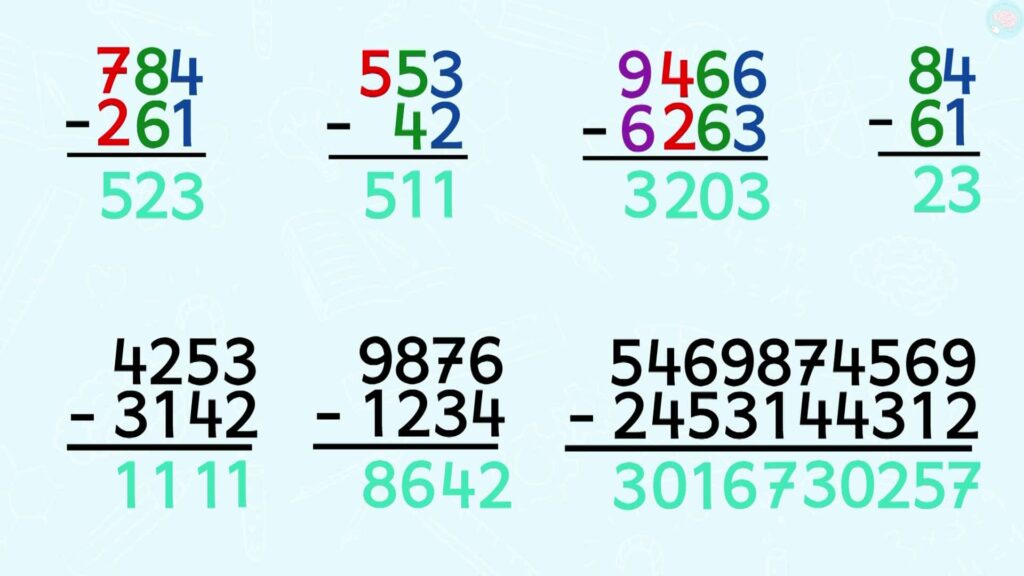
Je commence avec ce calcul. 4 — 1, 3, 8 – 6, 2, 7 – 2, 5, 523. Ensuite, 3 – 2, 1, 5 – 4, 1, 5 – 0, 5, 511. Je continue, 6 – 3, 3, 6 – 6, 0, 4 – 2, 2, 9 – 6, 3, 3203. Ensuite, 4 – 1, 3, 8 – 6, 2, 23. J’arrive en dessous avec de plus grands nombres et j’ai enlevé les couleurs, 3 – 2, 1, 5 – 4, 1, 2 – 1, 1, 4 – 3, 1, 1111. Si tu n’arrives pas à lire les grands nombres, ne t’inquiète pas, c’est juste pour te montrer que la technique ne change pas. Je continue, 6 – 4, 2, 7 – 3, 4, 8 – 2, 6, 9 – 1, 8, 8642. Et le dernier, 9 – 2, 7, 6 – 1, 5, 5 – 3, 2, 4 – 4, 0, 7 – 4, 3, 8 – 1, 7, 9 – 3, 6, 6 – 5, 1, 4 – 4, 0, 5 – 2, 3, 3 016 730 257. Eh ben ouai, je ne serais jamais arrivé à le lire. Effectivement, les très grands nombres, tu les verras en CM1 et en CM2.

Dans cette vidéo, nous avons appris à faire des soustractions posées sans retenue, bientôt nous parlerons des soustractions posées avec retenue, mais en attendant, tu peux t’entrainer sur cette fiche, qui est sur le site maitrelucas.fr sous cette vidéo. À très vite.




3 réponses sur « Soustractions posées sans retenue »
Bonjour,
Merci pour vos articles, leçons, fiches, exercices, .. : c’est clair, bien expliqué.
Je me permets de corriger :
“Faire le calcul avec une soustractions posées sans retenues” : merci de retirer les s à soustractions posées puisqu’il n’y en a qu’une.. !
Bonjour, merci pour votre vigilance. J’ai corrigé l’erreur.
Maître Lucas
Et ge ne savai pas tout sa wow