Il y a 4603 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
Fiche d’exercices
Télécharge la fiche d’exercices pour t’entrainer :
DESCRIPTION
Soustractions posées avec retenue
L’objectif de cette vidéo est d’apprendre à poser des soustractions en colonnes avec retenue. Les élèves de CE1 et CE2 pourront découvrir la méthode française traditionnelle (ou méthode par compensation) qui consiste à ajouter un même nombre. La méthode anglo-saxonne (par emprunt, par cassage) consiste à emprunter une dizaine. Généralement, je laisse les élèves choisir la méthode qu’ils préfèrent.
Cependant, chacune a ses qualités et ses défauts. La méthode traditionnelle est intéressante lorsqu’il y a une opération avec de nombreuses retenues mais le sens est plus difficile à saisir. La méthode anglo-saxonne est plus facile à expliquer avec du matériel mais nécessite de la place lorsqu’il y a plusieurs retenues.
LE CONSEIL DE MAITRE LUCAS
Proposer un problème avant un calcul
Les soustractions posées ne sont pas à utiliser quand les calculs sont faisables de tête. Elles doivent également toujours avoir du sens et être liées à la résolution de problèmes. Avant de proposer un calcul, n’hésitez pas à proposer un problème avec les nombres qui seront utilisés.
Compétences acquises
- Mettre en œuvre un algorithme de calcul posé pour la soustraction.
À qui s’adresse cette vidéo ?
Niveau
CE1 (Cours élémentaire 1ère année)
CE2 (Cours élémentaire 2ème année)
Matière
Maths, Mathématiques
Cours
Nombres et calculs, Soustractions
Soustractions posées avec retenue, c’est quoi ?
Si je fais cette soustraction, je commence par les unités, je fais 4 – 6, — 6, je ne peux pas enlever 6 à 4 ! Attends, il y a un problème, mais si je fais 6 pour aller à 4, ça ne marche pas non plus ! Maître Lucas ! Oula que se passe-t-il ? Eh bien, j’avais 94 euros et j’ai acheté un jeu pour ma SWITCH à 56 euros et j’aimerais bien savoir combien il me reste d’argent, donc je fais 94 – 56. Oui OK très bien, tu as enlevé les sous que tu as dépensés.
Je n’y arrivais pas de tête alors j’ai utilisé ta technique pour faire des soustractions posées sans retenue, mais je suis bloqué à 4 – 6. On est d’accord, on ne peut pas faire 4 – 6, non ? On va apprendre tout de suite deux techniques pour faire ce genre de soustractions posées, c’est parti !


La méthode française ou méthode par compensation
Prenons ton exemple 94 – 56, on a une première méthode que l’on peut appeler méthode française traditionnelle ou méthode par compensation.
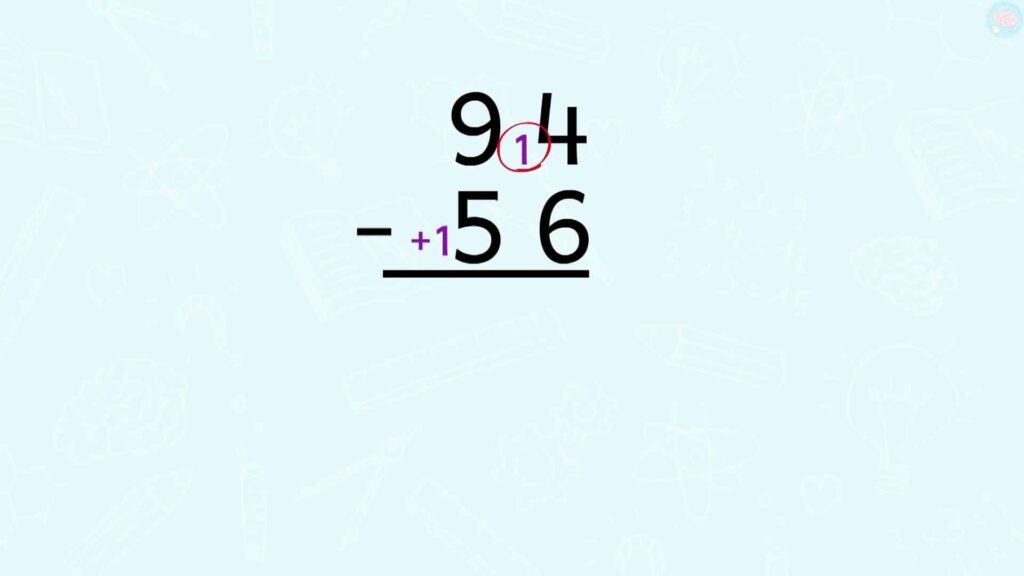
Comme tu ne peux pas faire 4 – 6 ou 6 pour aller à 4 ce n’est pas possible, alors tu ajoutes une dizaine ici pour faire 14 – 6 ou 6 pour aller à 14. Ah juste comme ça, je peux ajouter des dizaines où je veux ? Ah ben non évidemment ! Tu ne peux pas ajouter 10 comme tu veux. Si tu ajoutes 10 ici, tu dois aussi les ajouter là. Alors c’est comme s’ils s’annulaient.
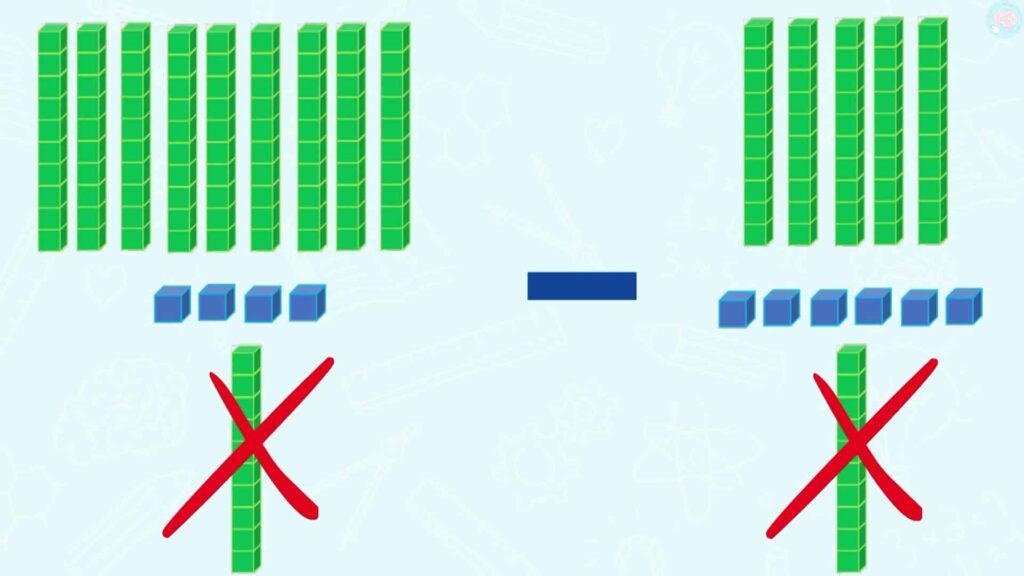
Regarde avec les cubes, ici j’ai 94, et ici 56. Si j’ajoute 10 unités ou une dizaine à 94 et aussi une dizaine à 56, et bien, quand je vais faire ma soustraction, toutes les deux vont s’annuler. Donc ça ne change rien au résultat, mais ça te permet de faire la soustraction.
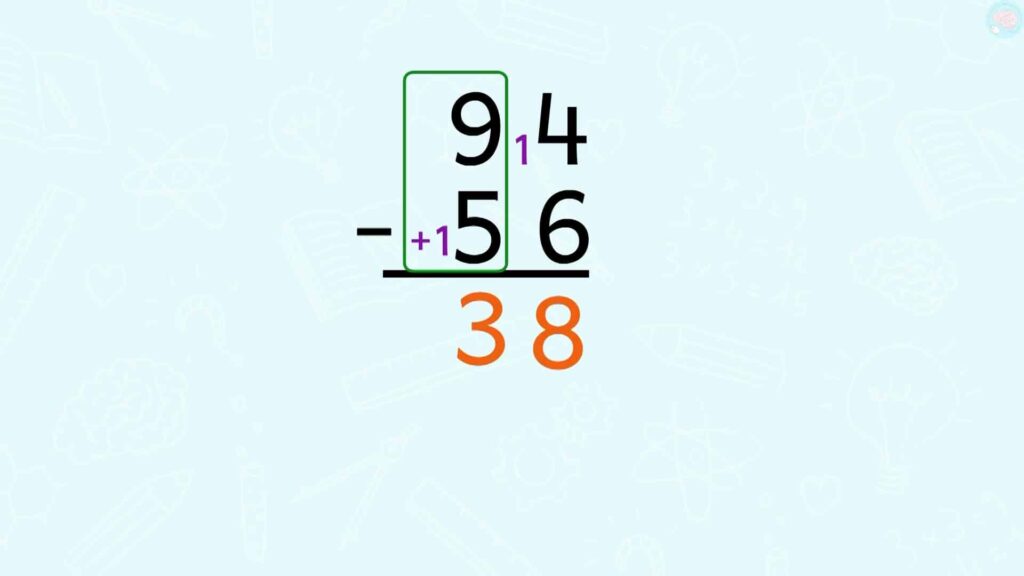
Je reviens à ma soustraction maintenant. Je peux faire 14 – 6, et ça fait 8. 6 pour aller à 14, ça fait 8. Ensuite, je ne fais pas 9 – 5, mais 9 – 6 puisque j’ai fait plus une dizaine. Et ça fait 3. Le résultat est donc 38, il te reste 38 euros.
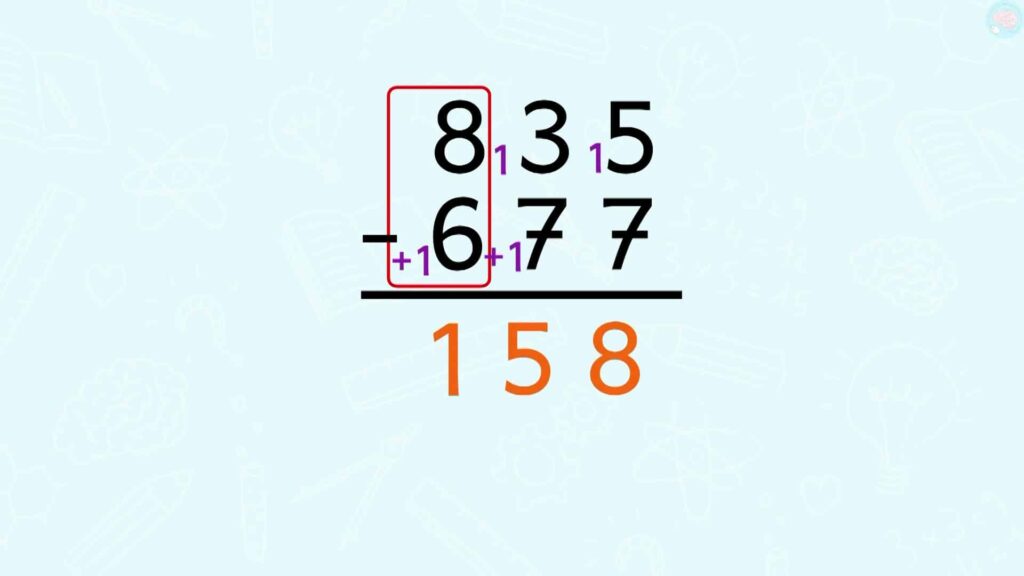
Je prends un exemple à trois chiffres 835 – 677, je commence par les unités comme d’habitude 5 – 7. Je ne peux pas, donc je rajoute 10, ça fait 15 ici et une dizaine là, +1. Ensuite, 15 – 7, ça fait 8. Puis je fais 3 – 8. Pourquoi 8, c’est écrit 7 ? J’ai ajouté une dizaine juste avant, regarde ici. Comme je ne peux pas faire 3 – 8, j’ajoute à nouveau +10 au 3, ça fait 13 et je n’oublie pas de l’ajouter ici.
13 — 8, ça fait 5, et enfin je termine 8 – 7, ça fait 1. Le résultat est 158.
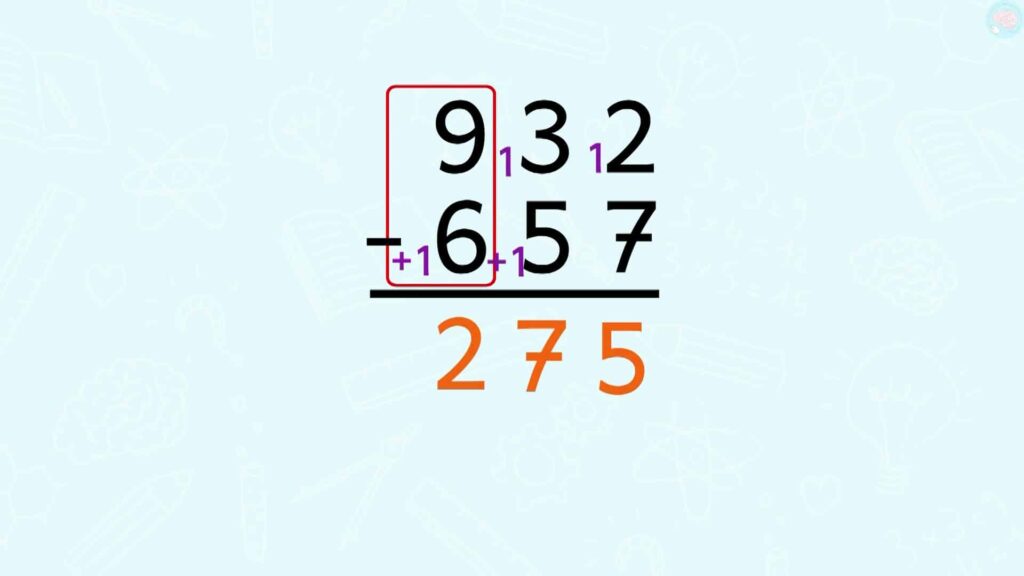
Un autre exemple, 932 – 657, je commence par les unités. 2 — 7, pas possible. Je fais +10, et j’ajoute une dizaine. 12 — 7, ça fait 5. Ensuite, 3 – 6, pas possible, je fais +10 ici, et je n’oublie pas de l’ajouter là. 13 — 6, ça fait 7. Et je termine par 9 – 7, ça fait 2. 275.
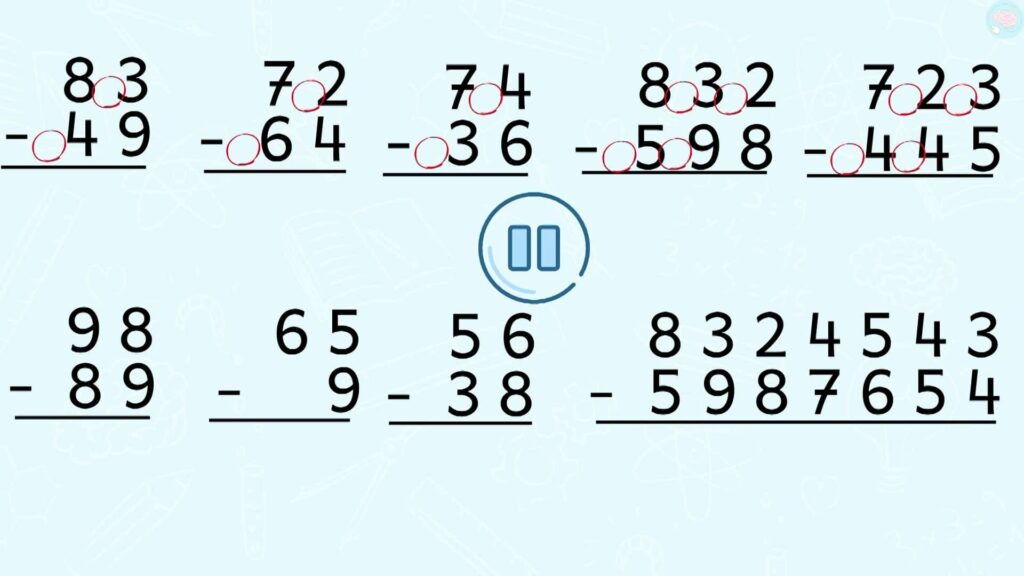
Exercices sur les soustractions posées avec retenue
Maintenant, je te propose plusieurs calculs pour t’entrainer pour que la technique reste bien dans ta tête. Tu peux les faire sur une ardoise ou une feuille. Dans les premiers calculs, je t’ai mis des petits cercles pour t’aider à bien mettre toutes les +10 que tu ajoutes. Ensuite, je ne les mets plus, et à toi de les retrouver. Mets pause sur la vidéo, car je vais bientôt donner les réponses.
Réponse
Voilà les réponses. Compare avec ce que tu as écrit et si tu as des erreurs, essaie de comprendre d’où viennent les erreurs afin qu’elles te permettent d’apprendre. Mets pause et prends bien ton temps.
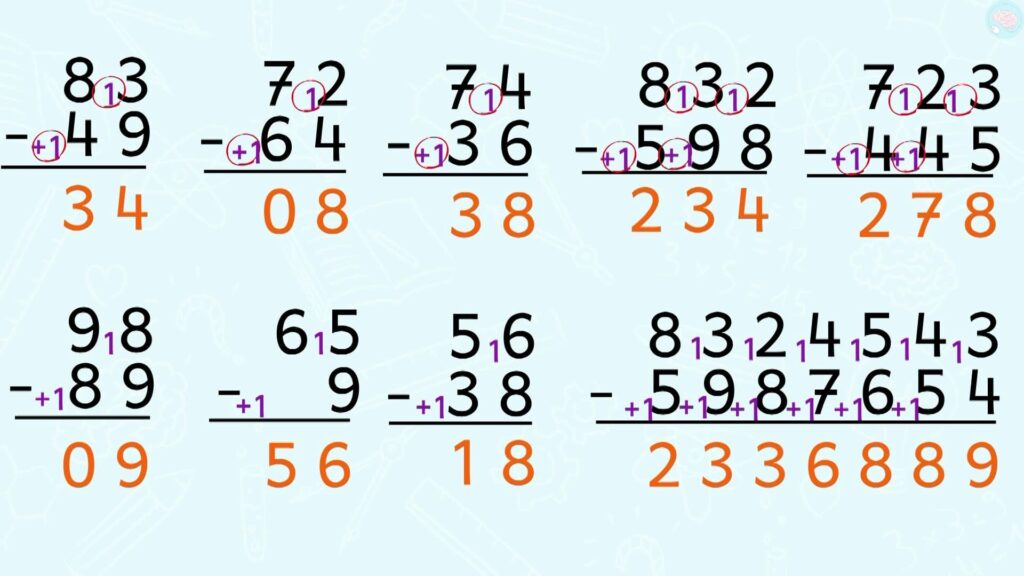

Attends, c’est déjà fini, mais tu m’as dit qu’il y a une autre technique non ? Oui effectivement il y a une autre technique, mais ça ne changera pas le résultat. La deuxième méthode on l’appelle Anglo-saxonne, par emprunt ou par cassage. Toi derrière ton écran, si tu as vu la 1re méthode en classe, tu peux arrêter la vidéo pour ne pas t’embrouiller et aller t’entrainer sur cette fiche, sinon tu peux continuer.

La méthode anglo-saxonne, par emprunt ou par cassage
Je reprends l’exemple des euros. Si je fais 94 – 56, je ne peux toujours pas faire 4 – 6.
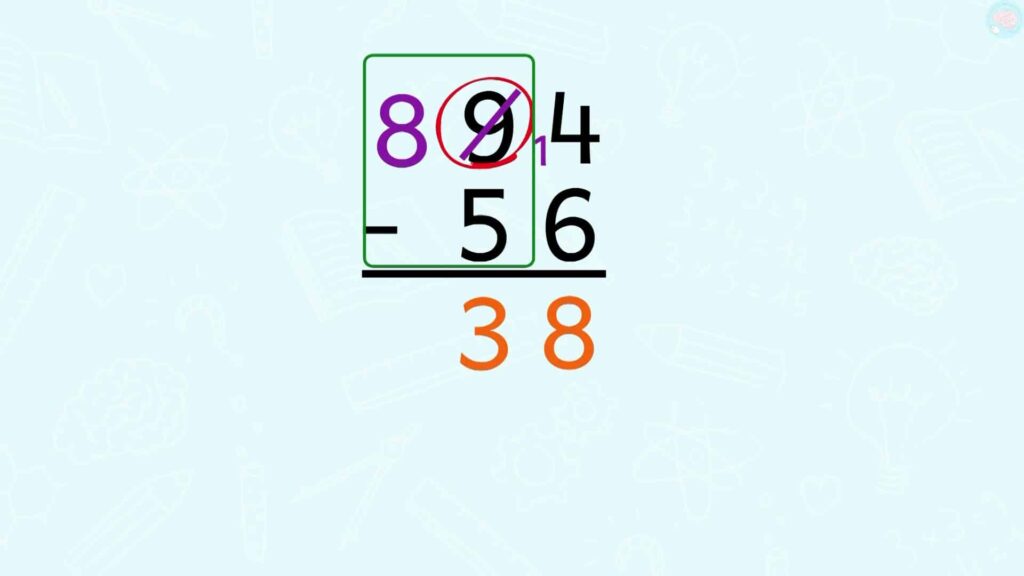
Tu sais quoi je vais piquer une dizaine ici, donc je barre 9 et j’écris 8. Et je vais l’ajouter là pour faire 14, c’est comme si tu empruntais une dizaine, et que tu la donnes à 4 pour faire 14. Maintenant comme avant, je fais 14 – 6, ça fait 8. Ici, il reste 8, puisque j’ai emprunté une dizaine. 8 — 5, ça fait 3. Donc le résultat est 38. On a le même résultat qu’avant. Voilà c’est l’autre méthode : avant j’ajoutai une dizaine en bas et au 4, maintenant j’en emprunte une en haut.
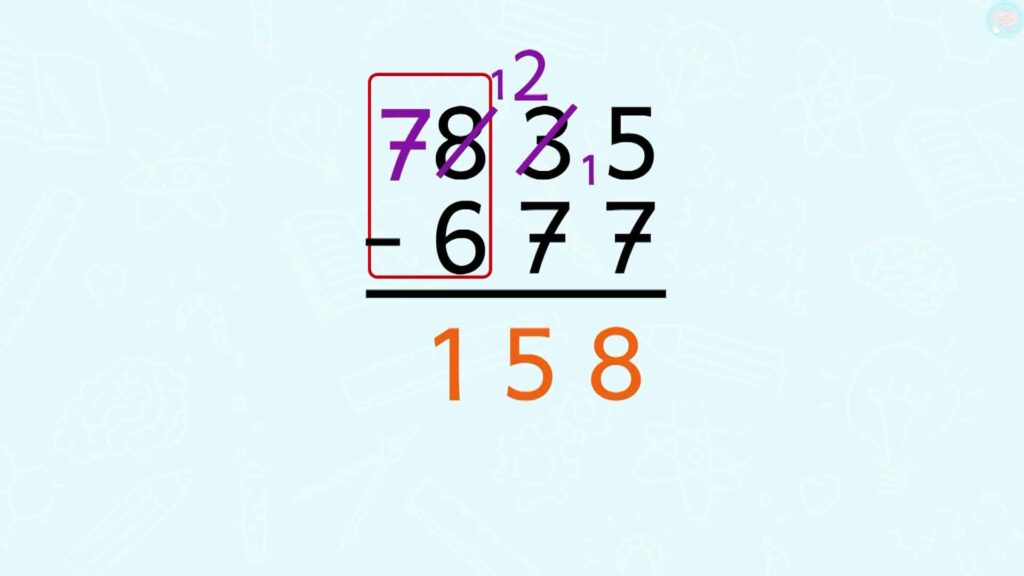
Je te montre à nouveau la technique avec un autre exemple. 835 — 677. 5 — 7, je ne peux pas alors j’emprunte une dizaine au 3, j’écris 2, puisque j’ai emprunté une dizaine et je la donne au 5. 15 — 7, ça fait 8. Ensuite, 2 – 7, je ne peux pas donc je dois aussi emprunter, mais cette fois-ci, une centaine au 8. J’enlève une centaine au 8, ça fait 7. 12 — 7 ça fait 5, puis le dernier 7 – 6, ça fait 1. Le résultat est 158.
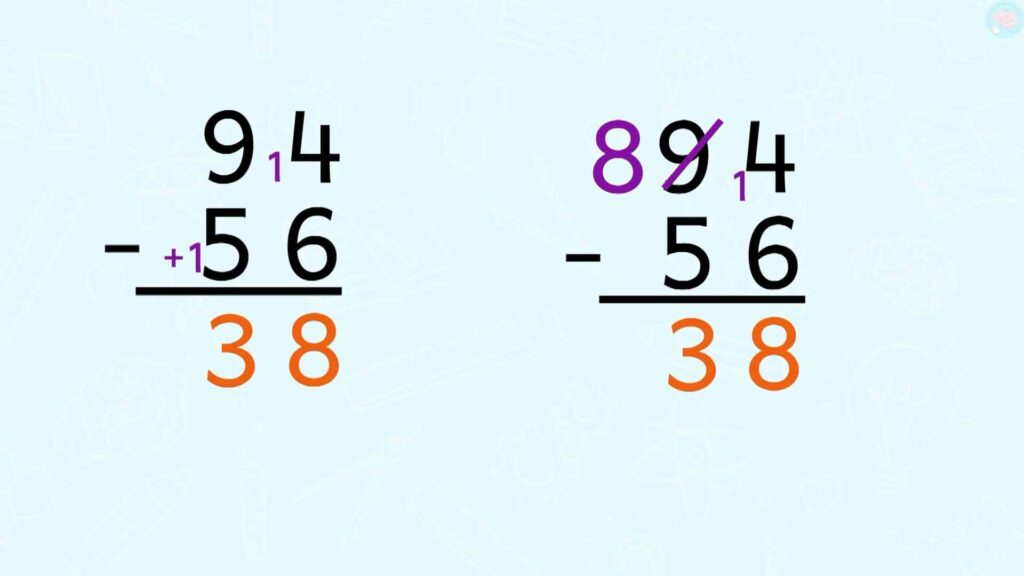
Donc fais bien attention, dans la première méthode, on ajoutait une dizaine ici et ici, alors que dans la deuxième on emprunte une dizaine là.
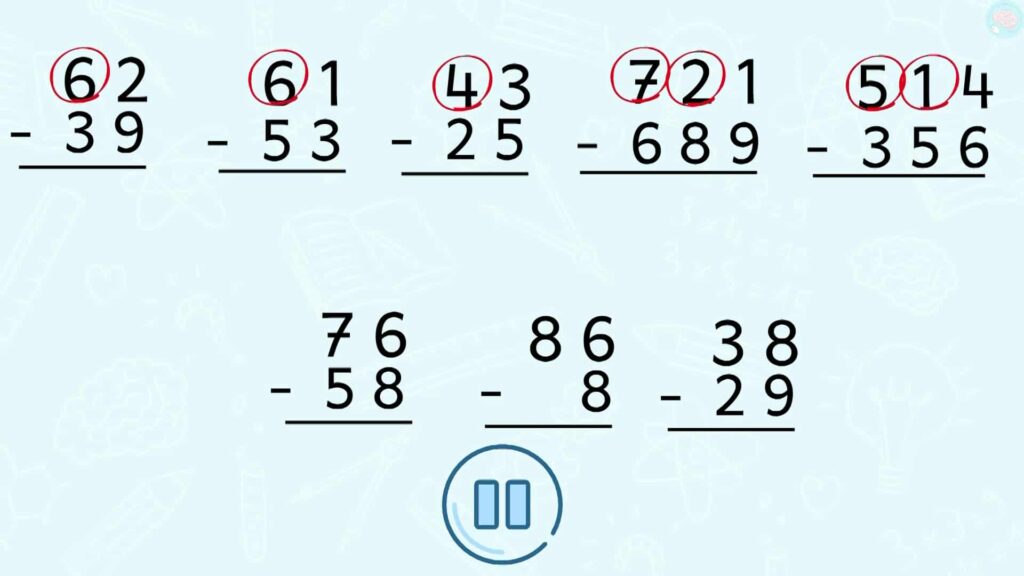
Exercices sur les soustractions posées avec retenue méthode anglo-saxonne
Comme avant il faut s’entrainer pour que ton cerveau retienne bien la méthode. Dans la première ligne des soustractions, je t’ai entouré là où il faut emprunter les dizaines. Mets pause sur la vidéo pour que tu aies le temps de toutes les faire.
Réponse
C’est bon terminé ? Voici les réponses. Comme avant mets, pause pour comparer avec ce que tu as écrit. Si tu as des erreurs et si tu veux que tes erreurs te servent à apprendre, il faut que tu cherches d’où elles viennent.
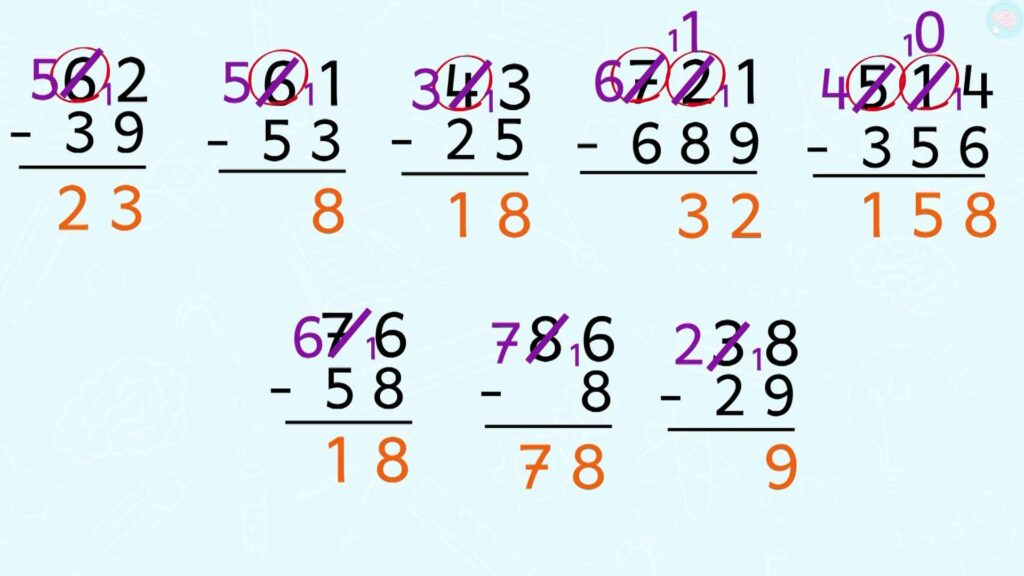

Dans cette vidéo, nous avons donc appris à poser des soustractions avec retenue et nous avons utilisé deux méthodes pour trouver les différences. Tu peux continuer à t’entrainer sur cette fiche qui est sur le site maitrelucas.fr sous cette vidéo. On se retrouve vite pour d’autres vidéos. À bientôt.



14 réponses sur « Soustractions posées avec retenue »
Bonjour Maître Lucas,
Je ne parviens à expliquer à ma fille, comment calculer en ligne (ou en arbre) les soustractions avec retenue.
Quels conseils pouvez-vous me donner, elle a une évaluation lundi 5.02 et elle est paniquée.
Merci
Un grand merci ! vos vidéos sont très claires.
Super vos vidéos ! Très inspirantes. Mais pour la soustraction avec retenues, on ajoute une dizaine en haut et une unité en bas et non une dizaine en bas?
Merci pour vos partages et bonne rentrée
Bonjour Brigitte,
Puisqu’on est dans le chiffre des dizaines c’est cohérent. Je dis bien que j’ajoute une dizaine à 7. Est-ce bien ça le problème ?
Bonne journée.
Maître Lucas
Bonjour. Je n arrive pas à expliquer clairement à ma fille comment poser en colonne une soustraction lorsque le 2ème nombre est plus important que le 1er. Ex :
168
– 196
_____
– 28
Bonjour,
Ce n’est malheureusement pas au programme en primaire. Je n’ai donc pas abordé le point.
Bonne journée.
Maître Lucas
Bonjour j’ai adoré votre vidéo je n’arrivé pas ,et maintenant j’i arrive
Merci pour la vidéo
Bravo !
merci beaucoup pour cette vidéo moi et ma mère nous avons adoré votre vidéo!
Merci beaucoup pour votre partage ! Je fais l’instruction à ma fille et je me rend compte que ce n’est pas si simple pour elle la méthode traditionnelle. En cherchant une solution pour l’aider, j’ai découvert votre leçon, je ne connaissais pas la méthode par cassage qui me paraît plus « logique » pour comprendre au départ. Je vais donc tenter celle-ci, merci ! 🙂
une bonne explication pour se rappeler ,à 76 ans,comment expliquer à ma petite fille ce que je fait, sans réfléchir depuis 70 ans ,merci
Bonjour. Ma petite fille de 8 ans a beaucoup de mal avec les soustractions. Je comprends un peu son problème concernant la méthode traditionnelle : lorsque le premier nombre est inférieur au 2ème, pourquoi on ajoute une dizaine aux unités et une unité aux dizaines. Je pense que la méthode anglo saxonne est plus compréhensible pour elle. Merci de l’avoir proposée.
Bonjour Lucas !
oui, je confirme, vos vidéos sont au top et c’est une instit à la ratraite , et maintenant mamie qui le dit , merci pour le partage devotre formidable travail ! Eve
Je trouve ce que vous faites absolument génial ! Je fais du soutien scolaire pour un élève de CP et votre partage m’aide à proposer du contenu. Merci !