Multiples et diviseurs

Identifier un multiple

Pour trouver les multiples d’un nombre, il suffit de le multiplier par un autre nombre, par exemple, je prends 4, je le multiplie par 3, ça fait 12. Donc 12 est un multiple de 4. D’ailleurs pour trouver tous les multiples de 4, on compte de 4 en 4, 4 8 12 16 20 24 28 32 36 40 44, etc. Mais ça ne s’arrête jamais ? Eh bien oui, effectivement un nombre à une infinité de multiples.

Un autre exemple avec 3, 3 6 9 12 15 18 21, etc. sont tous des multiples de 3.

Regardons quelques multiples de 5 par exemple. 5 10 15 20 25 30 35 40 45 50 55 60 et je m’arrête là. Est-ce que 43 est un multiple de 5 ? Euh attends, je le cherche. Il n’est pas là, donc je dirais non. Eh bien oui, 43 n’est pas un multiple de 5, en multipliant 5 par un nombre entier, tu ne peux pas tomber sur 43.

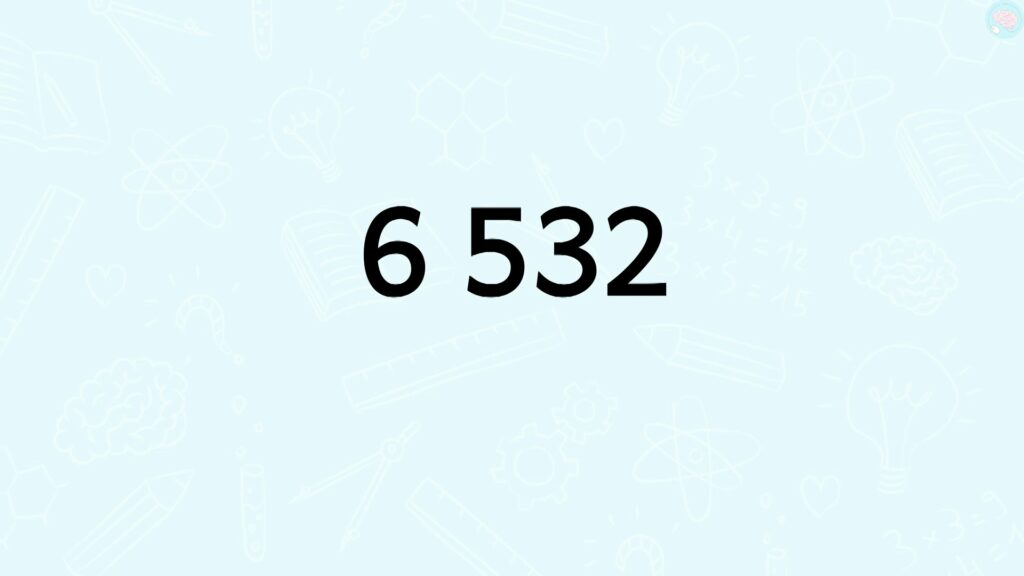
D’accord, j’ai compris. Bon, je vais chercher si 6532 est un multiple de 5. 5 10 15 35. Ha, mais attends attends, ça va être trop long. Bah, je n’ai pas le choix… Eh bien si, il y a une astuce pour trouver facilement si un nombre est un multiple de 5.

Identifier facilement les multiples de 2, 3, 5, 9 et 10

Mais avant, commençons par 2. Tous les multiples de 2 finissent par 0 2 4 6 8. Eh, c’est les nombres pairs. Exactement, donc 558 est un nombre pair et c’est un multiple de 2.

Un nombre est un multiple de 3 quand la somme de ses chiffres est un multiple de 3. Par exemple 636, j’additionne les chiffres 6 + 3 + 6, ça fait 15. Et comme 15 est un multiple de 3 et bien 636 aussi.

Un nombre est un multiple de 5, s’il se termine par 0 ou 5, par exemple 35 625 se termine par 5, donc c’est un multiple de 5.

Un nombre est un multiple de 9 si la somme de ses chiffres est un multiple de 9. Eh comme le 3 ! Oui, ça fonctionne de la même manière. Par exemple, 7452, 7 + 4 + 5 + 2 = 18, et comme 18 est un multiple de 9 alors 7452 aussi.

Un nombre est un multiple de 10 s’il se termine par zéro et on s’arrête là, on parlera de 4 et de 8 plus tard.

On peut avoir des nombres qui sont des multiples de plusieurs nombres, par exemple, 720 est un multiple de 2 3 5 9 et 10.

Exercices sur les multiples

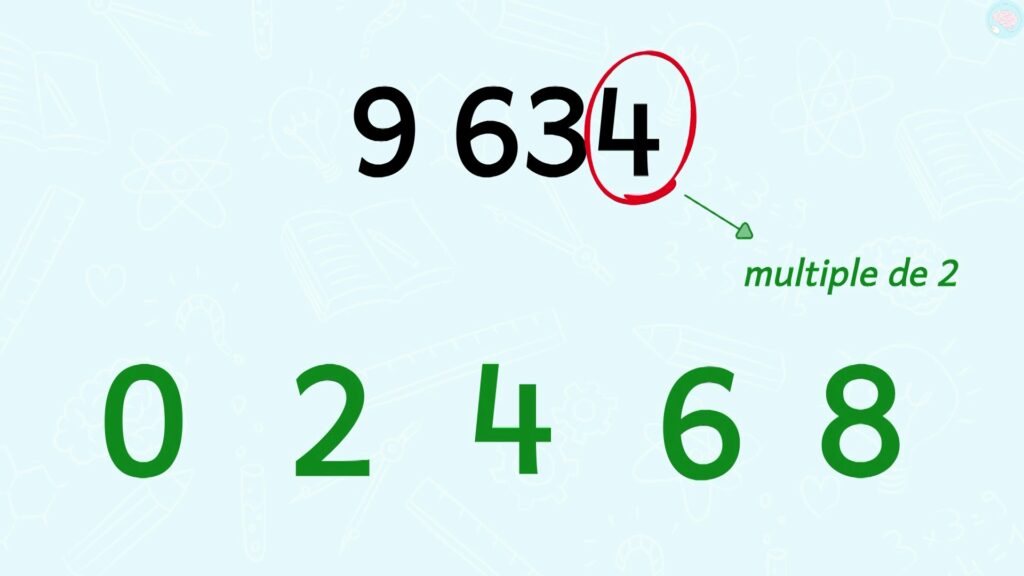
Toi derrière ton écran, peux-tu me dire si 9634 est un multiple de 2 ? Mets pause si tu as besoin de réfléchir.

Réponse

Eh bien oui, car il se termine par 4 et les multiples de 2 se terminent par 0 2 4 6 et 8.

Et est-ce que 854 est un multiple de 3 ?

Réponse

Eh bien non, puisque 8 + 5 + 4 ça fait 17, et 17 n’est pas un multiple de 3.

Identifier un divisible

Je reviens à ton problème de poule renard vipère. Si tu dois diviser les 23 enfants en 3 équipes, on sait maintenant que 23 n’est pas un multiple de 3. S’il n’est pas un multiple de 3, il ne peut pas être divisé par 3 non plus. On dit alors que 23 n’est pas divisible par 3. Quand un nombre n’est pas divisible par un autre, il y a un reste et dans ton cas, ce sont les deux enfants ici.

Quand un nombre est divisible par un autre, il n’y a pas de reste. Si vous étiez 21 dans la classe, 21 est un multiple de 3, donc 21 est divisible par 3 et il n’y a pas de reste.

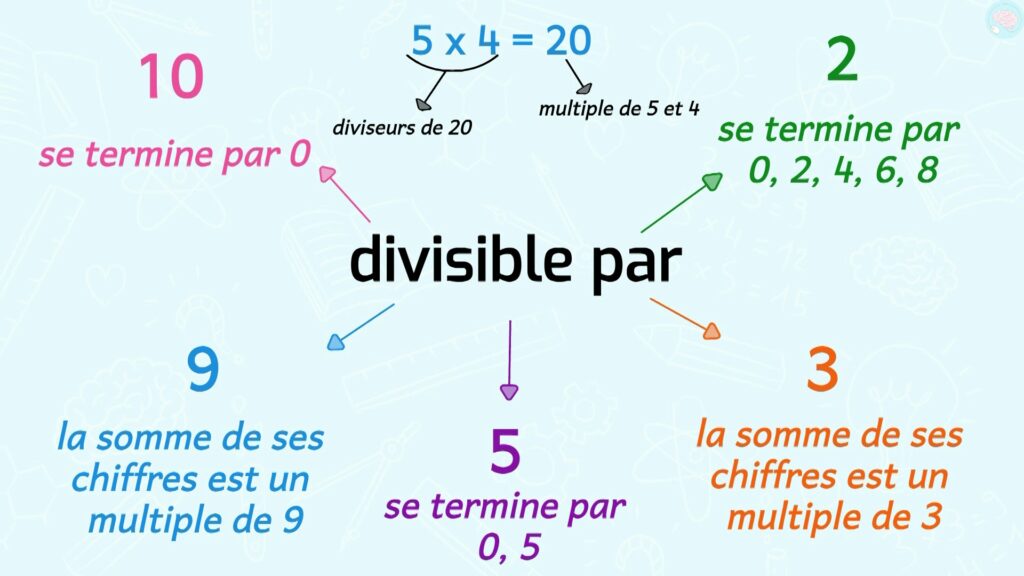
Regarde les critères pour savoir si un nombre est divisible par un autre. Mets pause si tu as besoin. Eh, mais attends, c’est la même chose que les multiples. Et bien oui, par exemple 5 x 4 ça fait 20, donc 20 est un multiple de 5 et de 4, mais 5 et 4 sont aussi des diviseurs de 20.

Exercices sur les diviseurs

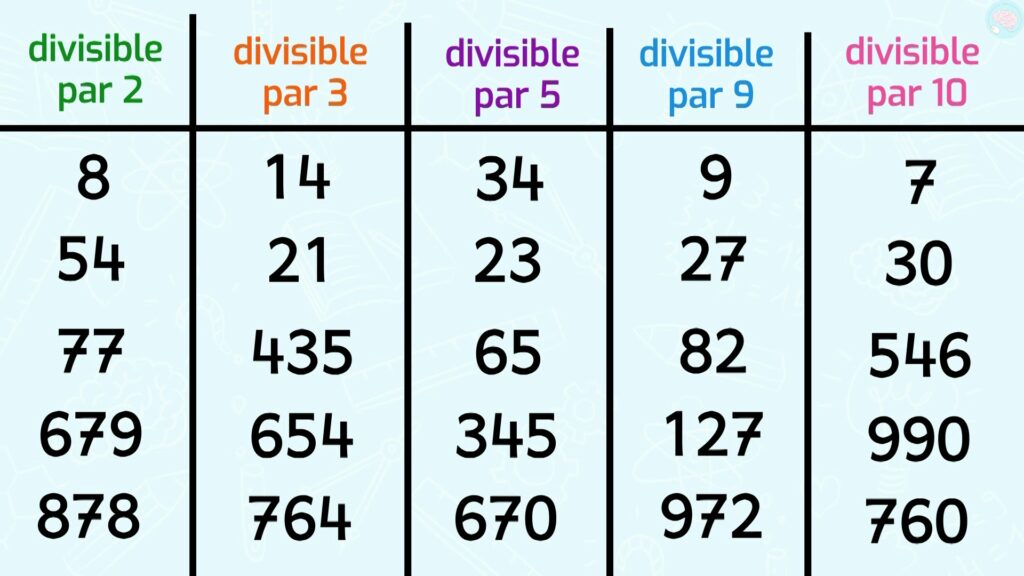
Maintenant un petit entraînement, trouve-moi dans chaque colonne les nombres qui sont divisibles par le nombre demandé. Ici, les nombres divisibles par 2, ici par 3 ici, par 5, etc. Mets la pause, c’est parti.

Réponse

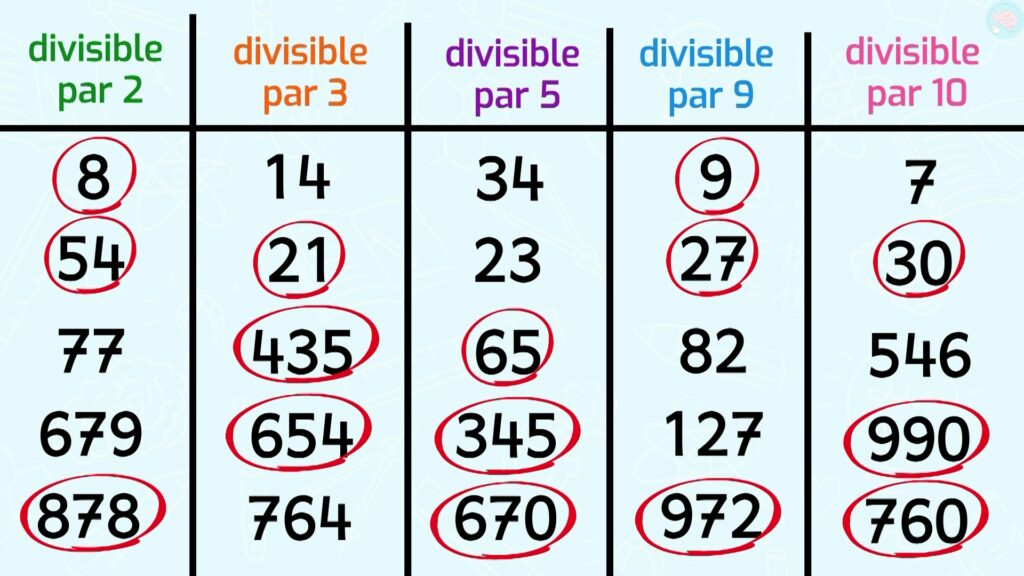
Et voilà les réponses, regarde bien les nombres que j’ai entourés et essaye de comprendre pourquoi. Si tu as des erreurs, n’oublie pas que les erreurs permettent d’apprendre quand on cherche d’où elles viennent.

Fiche d’exercices et carte mentale sur les multiples et diviseurs

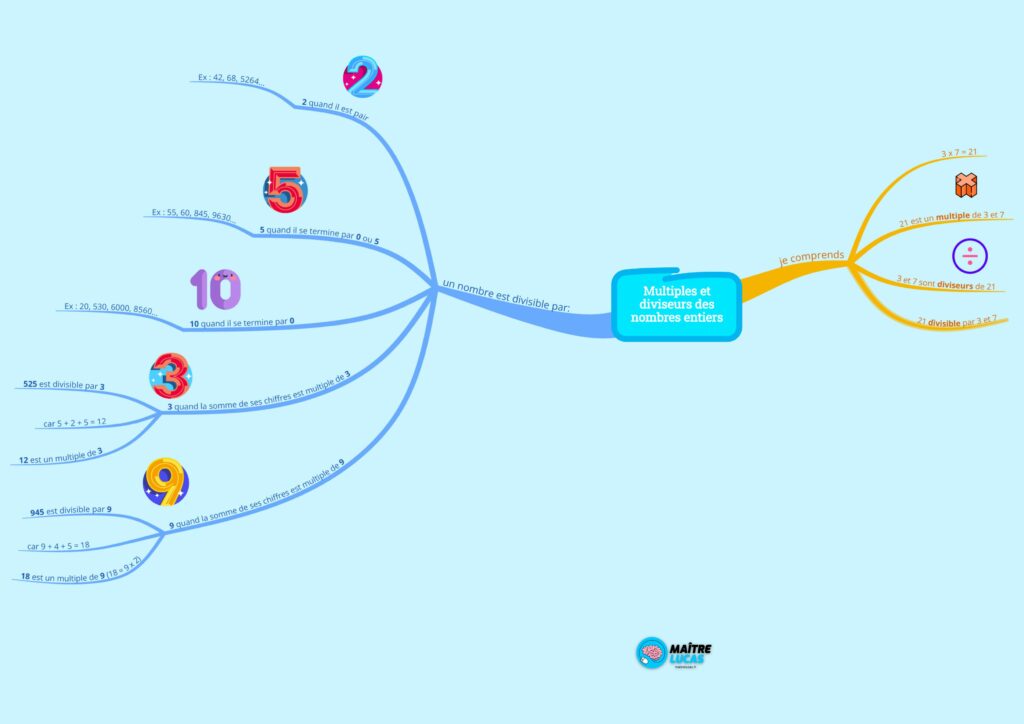
Tu sais maintenant comment trouver le multiple d’un nombre et comment savoir si un nombre est divisible par un autre. Bien sûr, il faudra un peu de temps pour retenir tout ça. En attendant, je t’ai préparé une carte mentale et une fiche d’exercice que tu retrouveras, bien sûr, sur le site maitrelucas.fr sous cette vidéo. À plus.