Il y a 8583 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
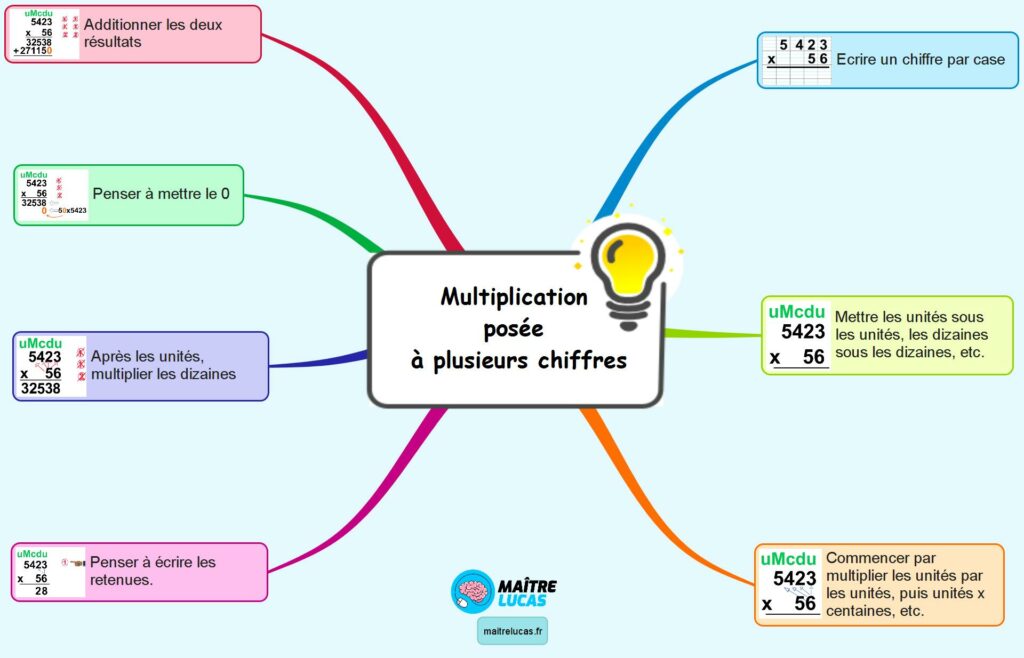
Carte mentale les multiplications posées à plusieurs chiffres
Fiche à télécharger
Télécharge la fiche à afficher chez toi afin de te souvenir de cette leçon
DESCRIPTION
Multiplications posées à plusieurs chiffres
Cette vidéo correspond à la compétence de mathématiques (attendue dans les programmes de cycle 3) suivante : “Connaître et mettre en œuvre un algorithme de calcul posé pour effectuer une multiplication”. Elle a donc pour but de maîtriser une technique permettant de trouver la réponse d’une multiplication posée à plusieurs chiffres. A travers des animations, j’ai tenté d’expliquer la démarche afin qu’elle puisse être reproduite.
LE CONSEIL DE MAITRE LUCAS
Écrire les 0
Au début, des apprentissages et afin de faciliter la tâche de votre enfant, vous pouvez lui écrire les 0 nécessaires, ainsi que les signes de l’addition afin qu’il ne les oublie pas. Au fur et à mesure vous pourrez les enlever.
Compétences acquises
- Connaître et mettre en œuvre un algorithme de calcul posé pour effectuer une multiplication.
- Résoudre une multiplication posée à plusieurs chiffres.
À qui s’adresse cette vidéo ?
Niveau
CM1 (Cours Moyen 1ère année)
CM2 (Cours Moyen 2ème année)
Matière
Mathématiques, Maths
Cours
Multiplications, nombres et calculs
Comment poser les multiplications plusieurs chiffres ?
Maître Lucas, tu m’as montré comment faire une multiplication à un chiffre, mais là j’ai deux chiffres. Je n’y arrive pas. Eh bien, je te propose d’en parler tout de suite.


Dans la vidéo précédente, je proposais une leçon sur les multiplications à un chiffre comme 548 x 6, il y a un chiffre ici. Maintenant, on passe à 2, 3, 4, 1 000 chiffres si tu veux.

Comment poser ses multiplications ?
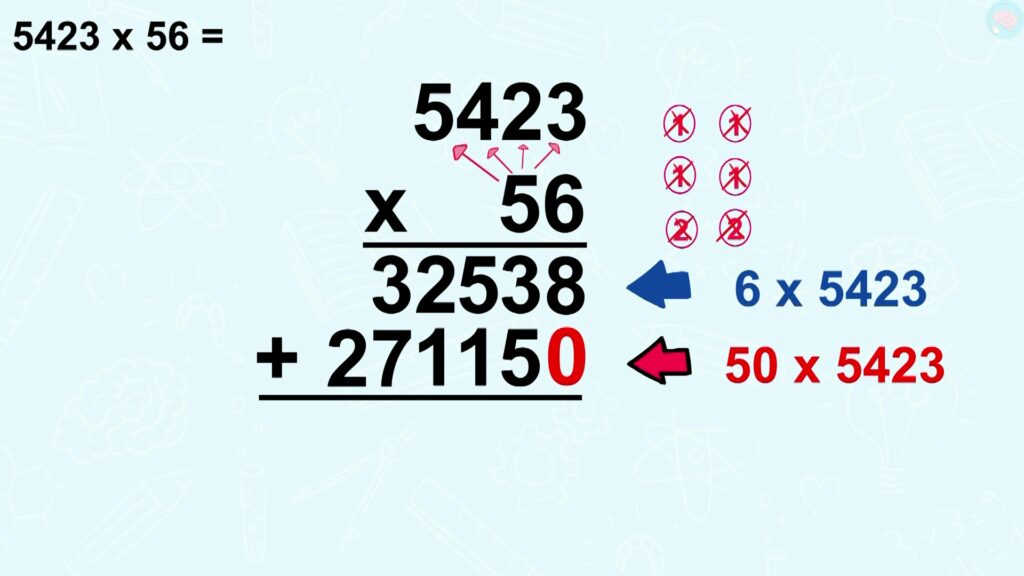
Et l’on commence avec le premier calcul, 5423 x 56. Ici, il y a deux chiffres.
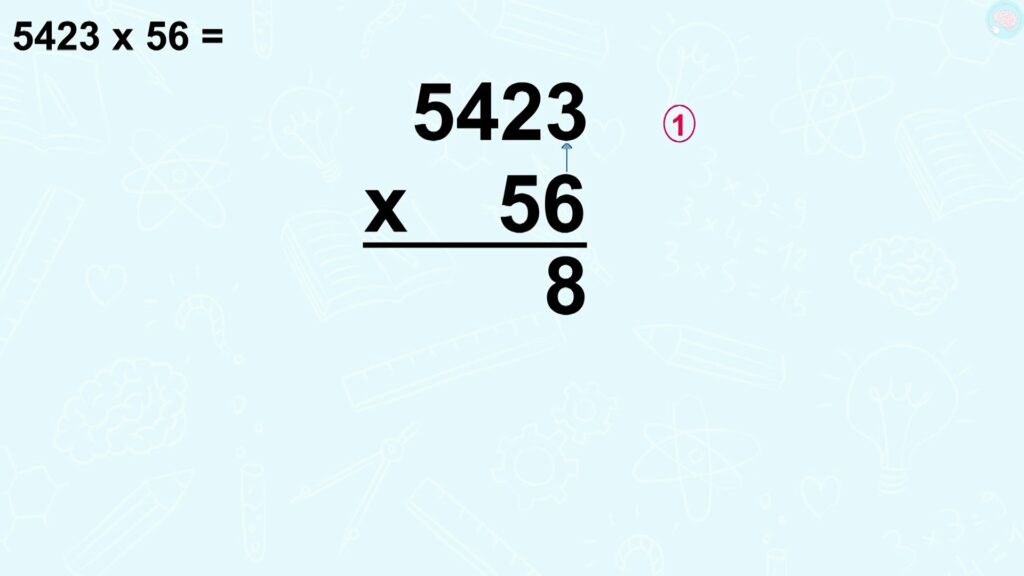
Comme pour les multiplications à un chiffre, on commence par les unités donc par 6, que je multiplie à tous les chiffres au-dessus. On fait d’abord 6 x 3, ensuite, 6 x 2, puis 6 x 4 et enfin 6 x 5.
Donc 6 x 3, combien est-ce que ça fait toi derrière ton écran ?
18, bien sûr, je note le 8 et je retiens le 1. Ensuite, 6 x 2 ça fait 12 je note 2 et je retiens 1.
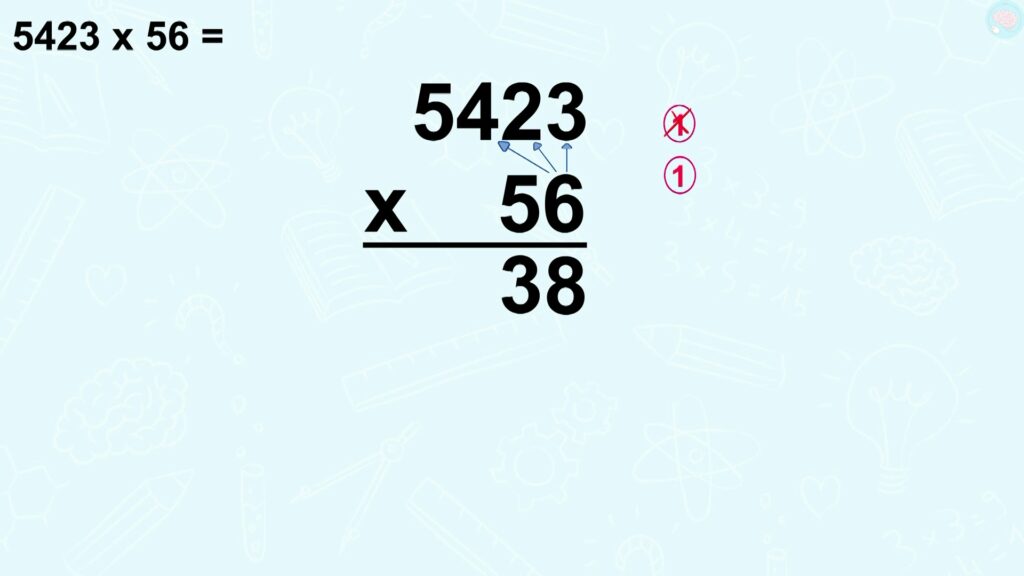
C’est bon ? C’est juste ? Eh bien non, j’ai fait une erreur. J’ai oublié d’ajouter la retenue d’avant. Je recommence 6 x 2, ça fait 12 et je rajoute le 1 de la retenue que je barre, car je l’ai utilisé, ça fait donc 13. J’écris 3 et je retiens 1.
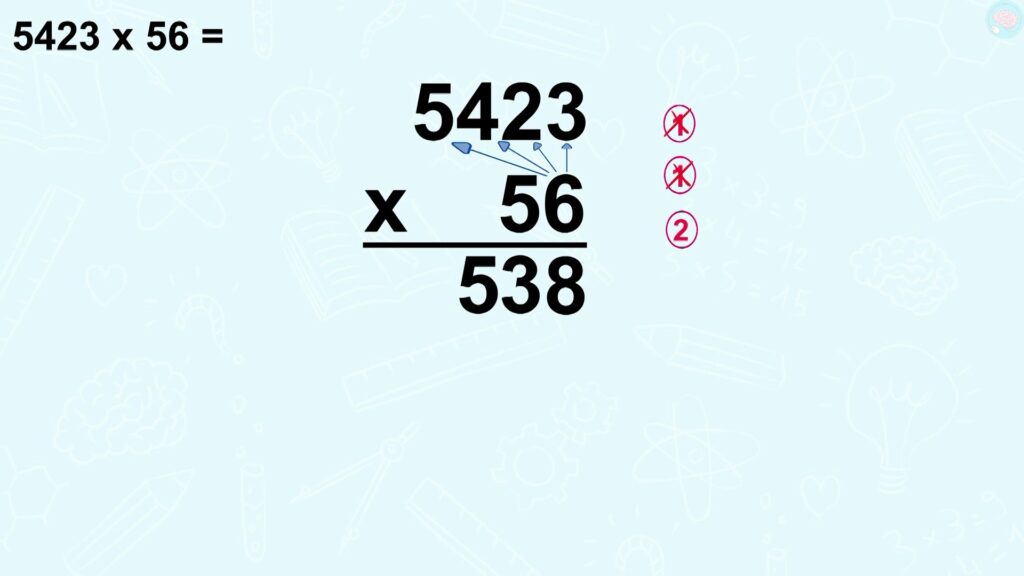
Ensuite, 6 x 4 ça fait combien ? Ça fait 24, je n’oublie pas la retenue, ça fait 25. Je note le 5 ici, et je retiens 2. Et le dernier, 6 x 5 ça fait 30 et j’ajoute bien entendu le 2 de la retenue. Donc 32. Le 32, je peux l’écrire en entier, pas besoin de retenue puisque le calcul est fini. Ouf, on a fini avec les unités avec le 6.
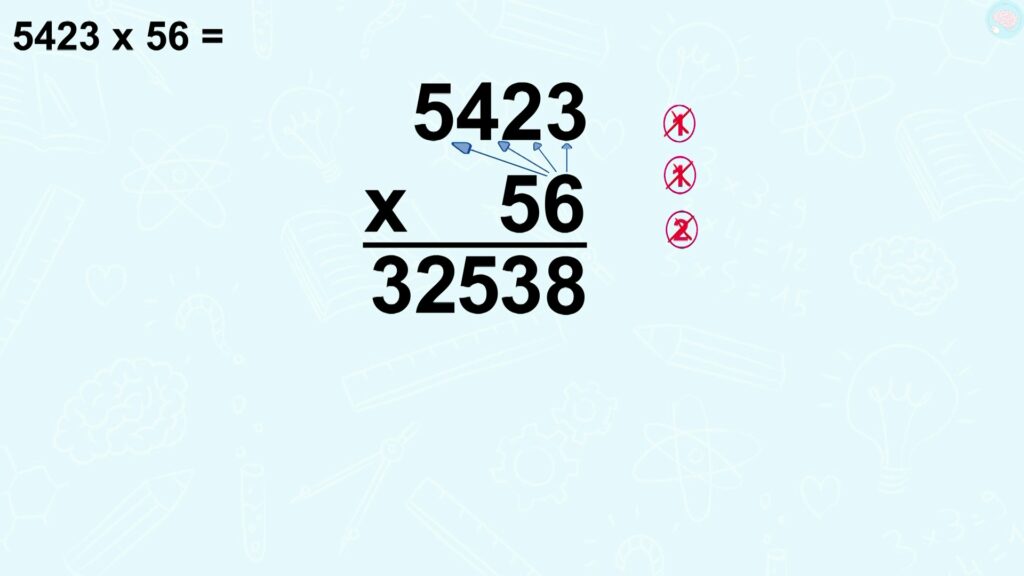
On doit maintenant attaquer les dizaines avec le 5. Mais je mets où les calculs, il n’y a plus de place ? C’est vrai, tu as raison, les calculs avec le 6 ont pris toute la place. Eh bien, je les mets tout simplement en dessous, ça veut dire que je vais commencer ici.
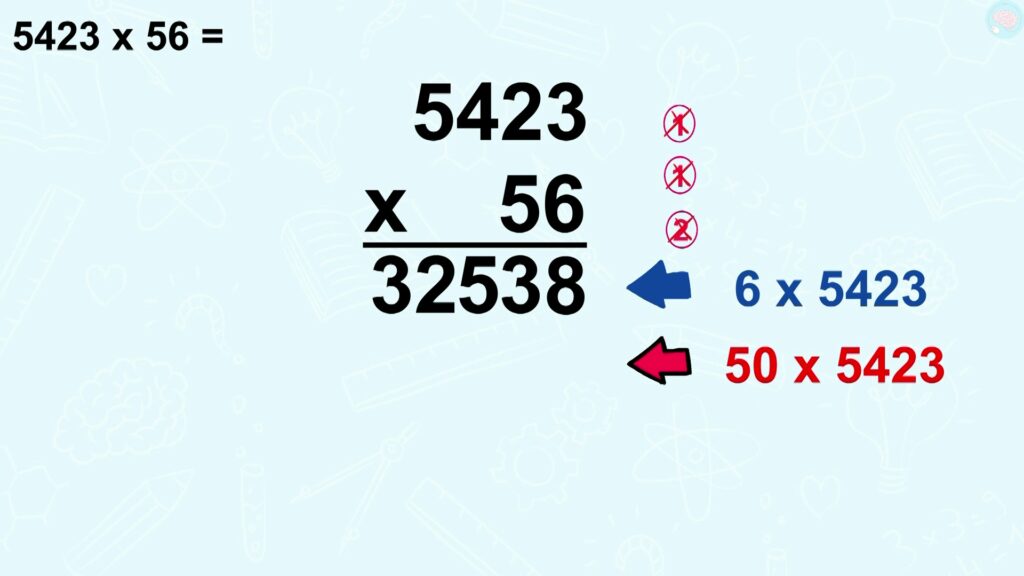
Multiplications posées à plusieurs chiffres, bien faire le seconde chiffre
Avant, nous avions fait 6 x 5423, et en dessous, je vais donc faire 50 x 5423. Pour que ce soit plus simple, je fais d’abord x 10, et ensuite, x 5.
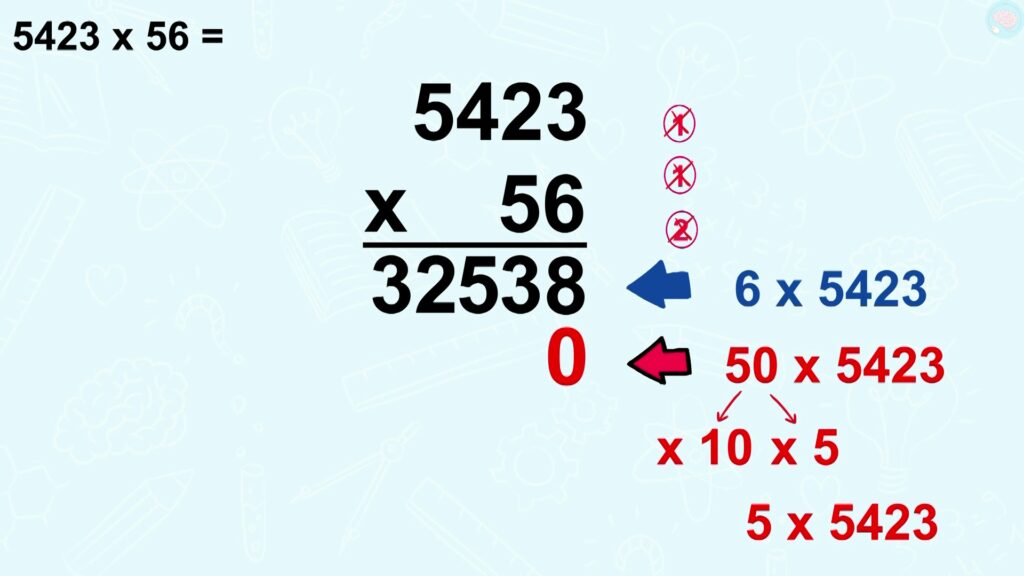
Comme je fais x 10, j’écris un 0 ici, et ensuite, il ne me reste plus qu’à faire 5 x 5423.
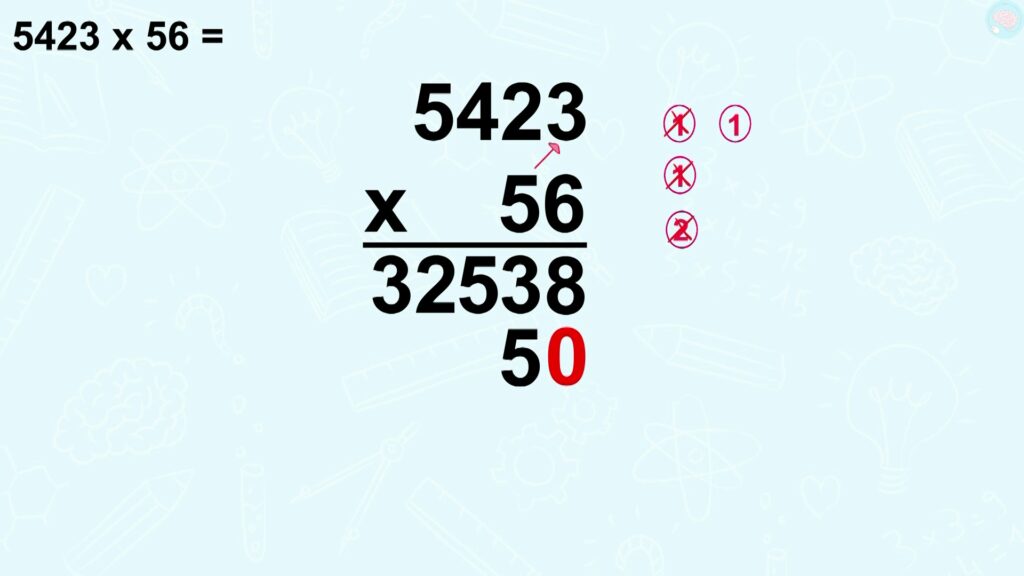
Allez c’est parti, j’accélère pour les calculs. Le premier, c’est 5 x 3, ça fait 15. J’écris 5 et je retiens 1.
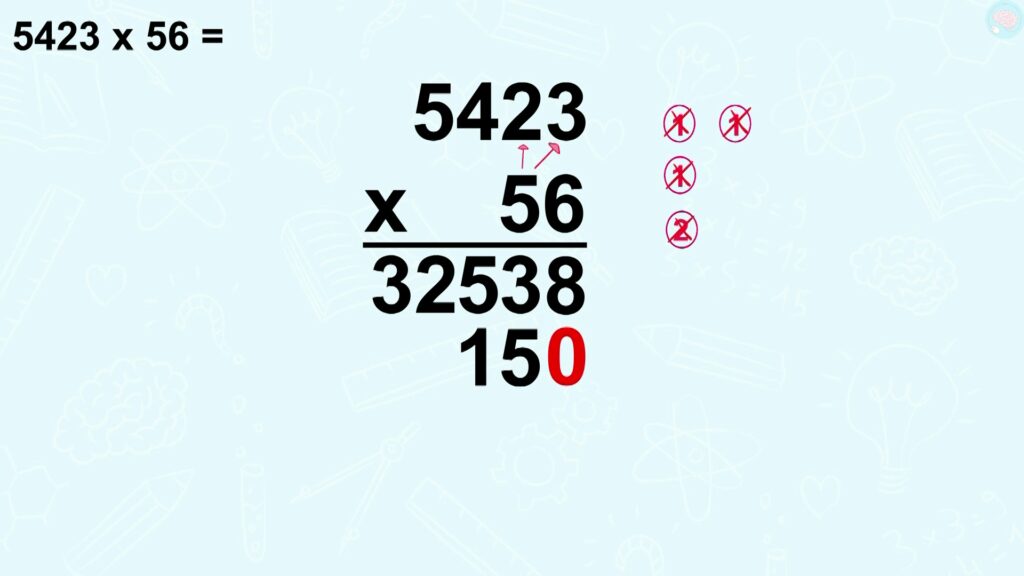
5 x 2, ça fait 10. Je n’oublie pas d’ajouter la retenue, ça fait 11. J’écris 1 et je retiens 1.
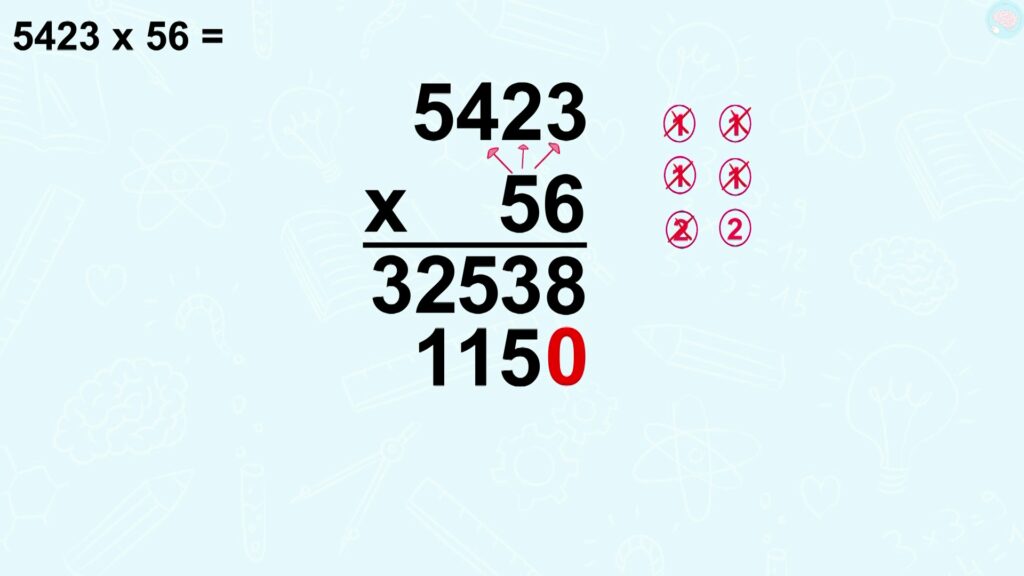
5 x 4, ça fait 20. J’ajoute la retenue, ça fait 21. J’écris le 1 et je retiens 2.
5 x 5, ça fait 25 + 2 de retenue donc 27, j’écris 27 puisque le calcul est fini.
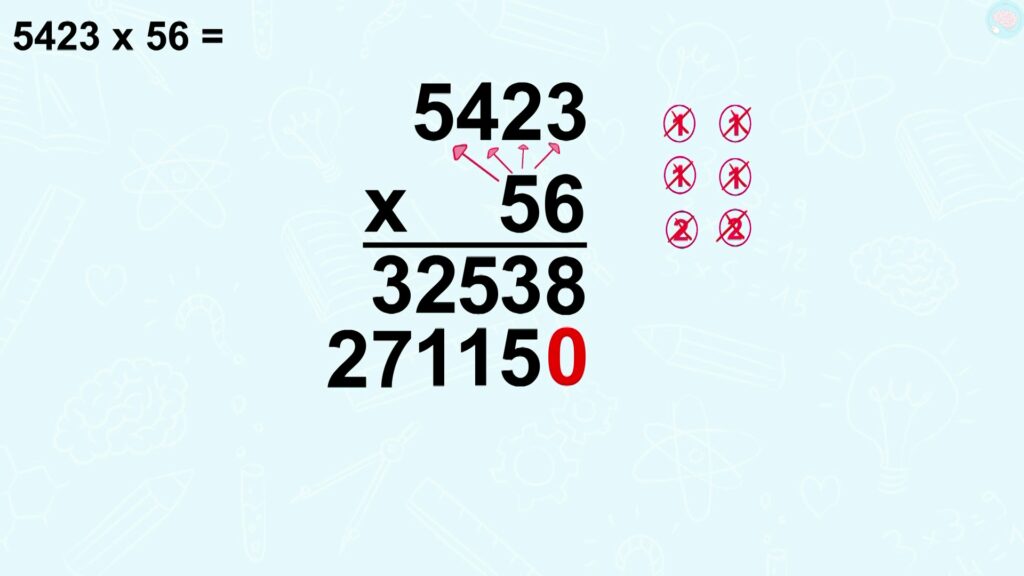
J’ai presque fini 6 x 5423, ça fait 32 538, et 50 x 5423 ça fait 271 150.
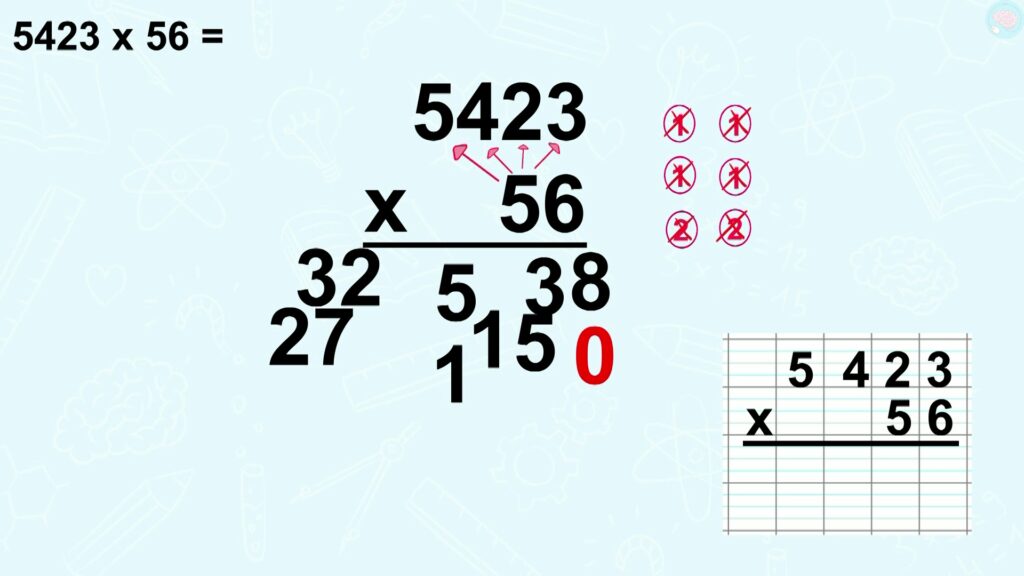
C’est important de bien séparer les chiffres, sinon tu vas te retrouver avec ça sur ta feuille et tu vas mélanger les calculs. Donc si tu écris sur une feuille à carreaux, un chiffre par case.
Additionner les résultats
Mais je voulais une réponse, pas 2 réponses. Oui, je n’ai toujours pas ma réponse finale. Je dois faire une dernière chose additionner les deux réponses. Je mets donc un plus ici, comme si je faisais une addition, je tire un trait comme si je faisais une addition aussi, et je commence.
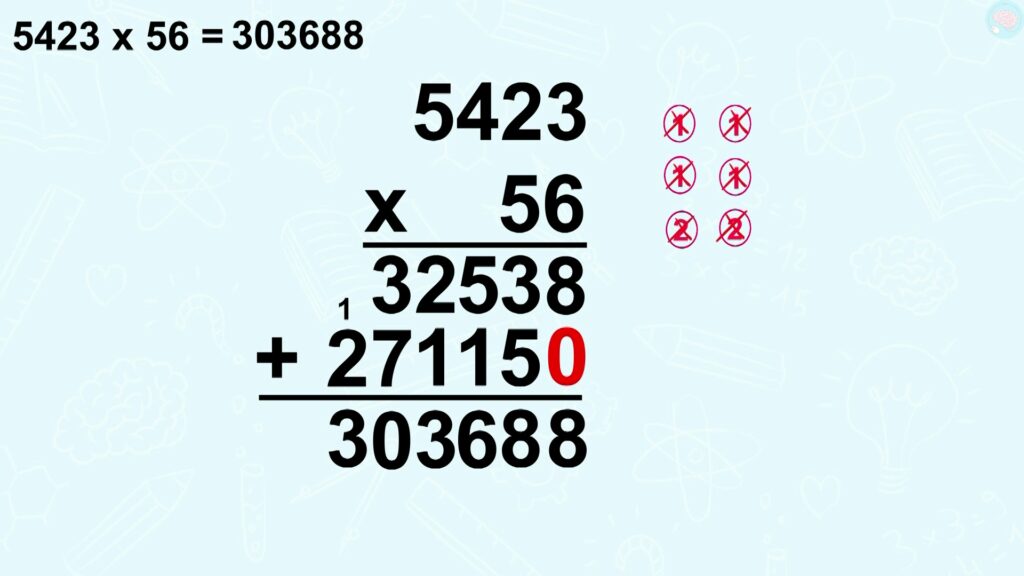
8 + 0, ça fait 8. 3 + 5 = 8. 5 + 1 = 6. 2 + 1 = 3, 3 + 7 = 10. J’écris 0, je retiens 1. La retenue + 2, ça fait 3. J’obtiens enfin ma réponse : 303 688. Ça y est, c’est fini. Tu as le résultat de la multiplication posée à deux chiffres.
Si c’était trop rapide pour toi, n’hésite pas à revoir la vidéo 1 000 fois s’il le faut. Si ça va, on va faire un autre exemple, mais cette fois-ci à 3 chiffres.

Les multiplications posées à 3 chiffres
6745 x 237, j’ai 3 chiffres ici. On commence par les unités comme toujours 7 x 5 = 35. J’écris 5, je retiens 3.
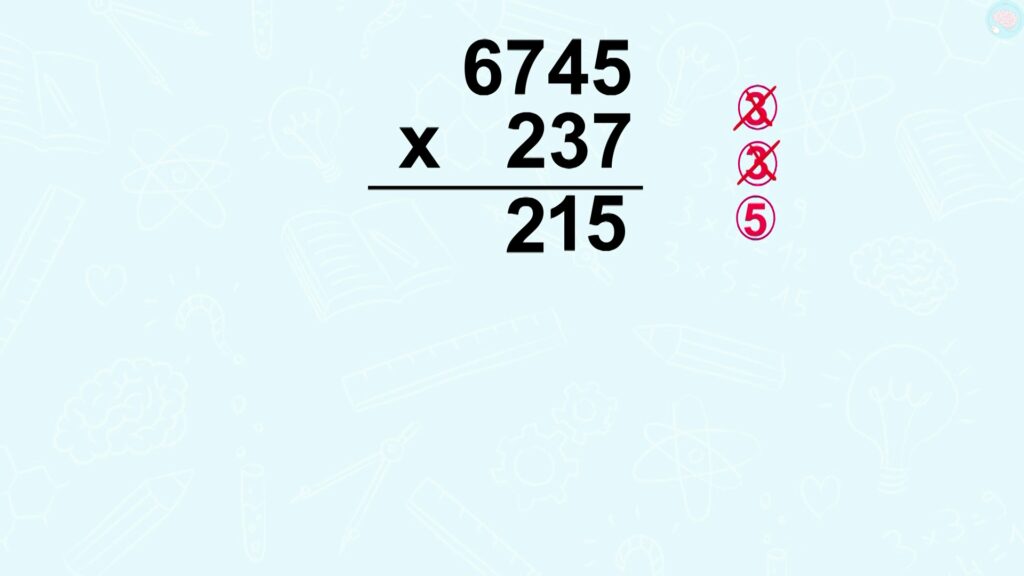
7 x 4 = 28, et j’ajoute le 3 de la retenue, 31. J’écris 1 et je retiens 3. 7 x 7 = 49, + la retenue, 52. J’écris 2 et je retiens 5.

7 x 7 = 49, + la retenue, 52. J’écris 2 et je retiens 5. 7 x 6 = 42, + la retenue, 47. J’écris le 47 en entier et c’est terminé pour 7 x 6745.
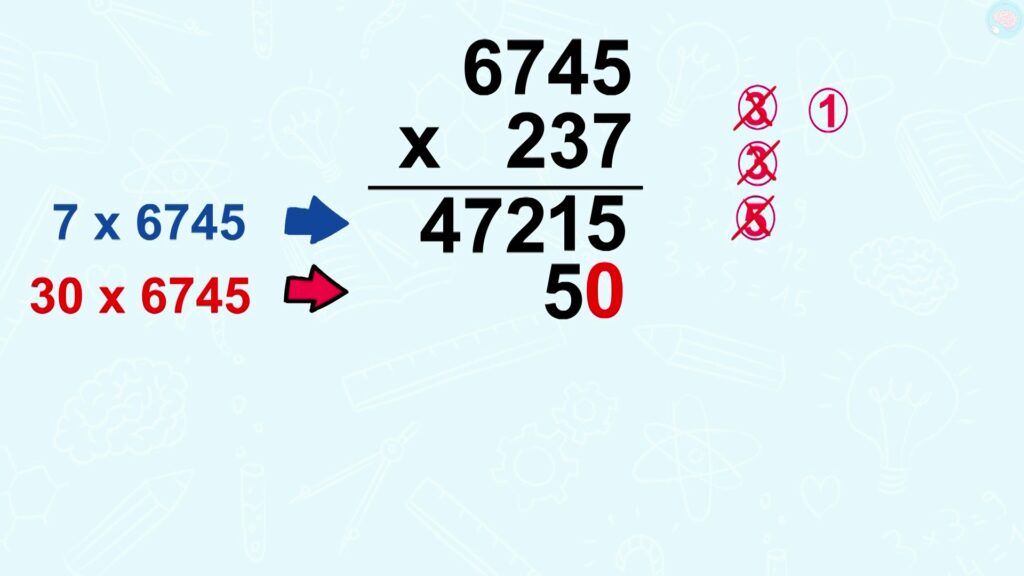
Ensuite, je fais 30 x 6745 et je n’oublie pas le 0, puisque je fais x 10 et x 3 au lieu de faire x 30. 3 x 5 = 15, j’écris 5 et je retiens 1.
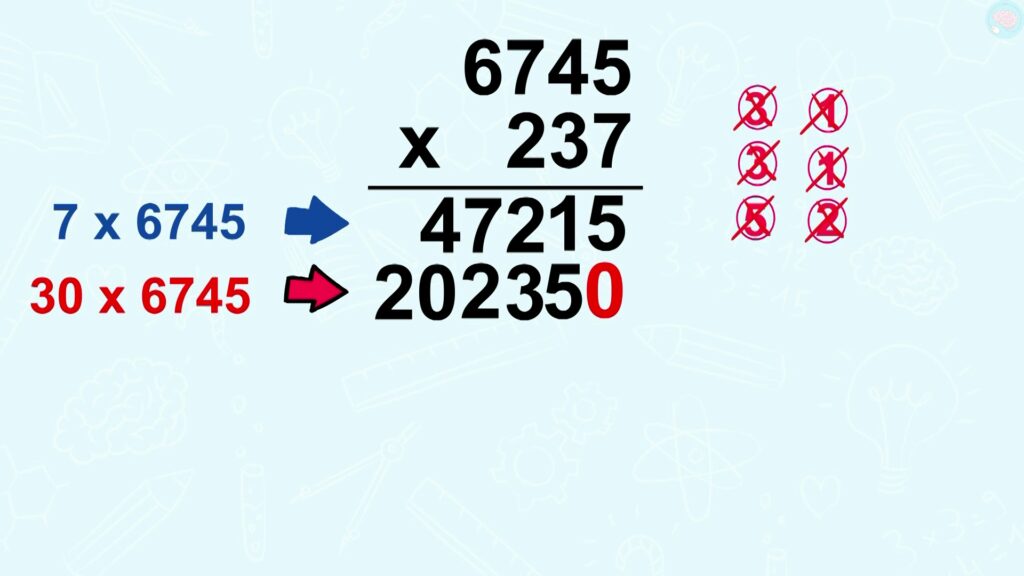
3 x 4 = 12, plus la retenue 13. J’écris 3, je retiens 1. 3 x 7 = 21 plus la retenue 22. J’écris 2, je retiens 2. 3 x 6 = 18, plus la retenue 20 et j’écris tout le 20, puisque c’est terminé.
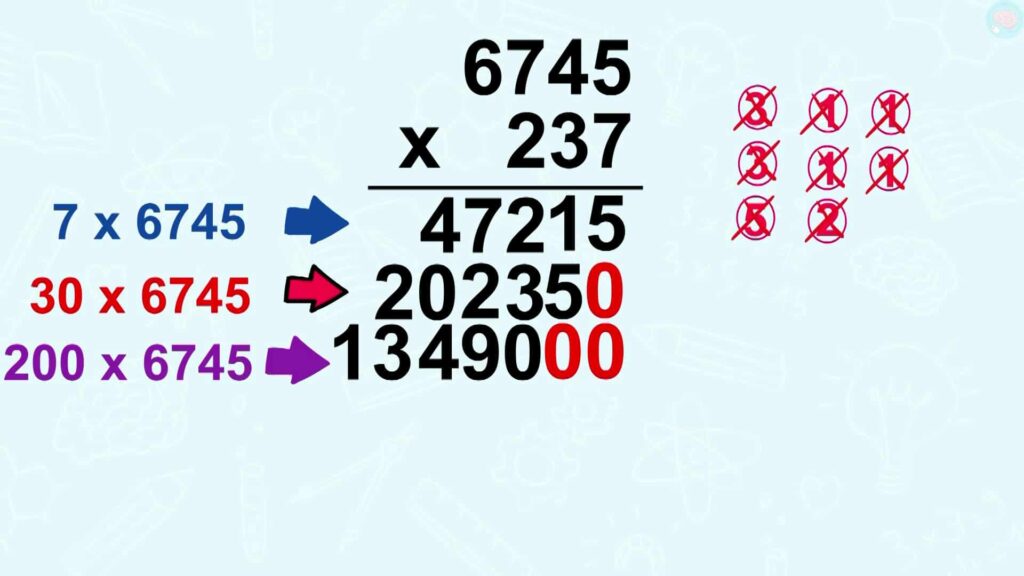
La multiplication posée à trois chiffres bien faire les centaines
Cette fois-ci, on a encore des centaines à effectuer avec le 2. Attends, ne me dis rien. On doit mettre deux 0 pour commencer en dessous de deux, parce qu’on fait 200 x 6745 ? C’est exactement ça, bien joué ! Donc rapidement, 2 x 5 = 10. J’écris 0, je retiens 1. 2 x 4 = 8, 8 +, la retenue, + 1 = 9, 2 x 7 = 14, j’écris 4, je retiens 1. 2 x 6 = 12, + 1 de la retenue = 13 et j’ai terminé.

Tu te souviens de ce que je dois faire après ? Eh bien, j’additionne les trois réponses. Je pense au « + » et à mon trait, et c’est parti. Je commence par les unités, 5 + 0 + 0 = 5, 1 + 5 + 0 = 6, 2 + 3 + 0 = 5, 7 + 2 + 9 = 18, j’écris 8, je retiens 1. La retenue + 4, + 4 = 9. 2 + 3 = 5 et 1, donc le résultat est 1 598 565.
Exercices sur les multiplications posées à plusieurs chiffres
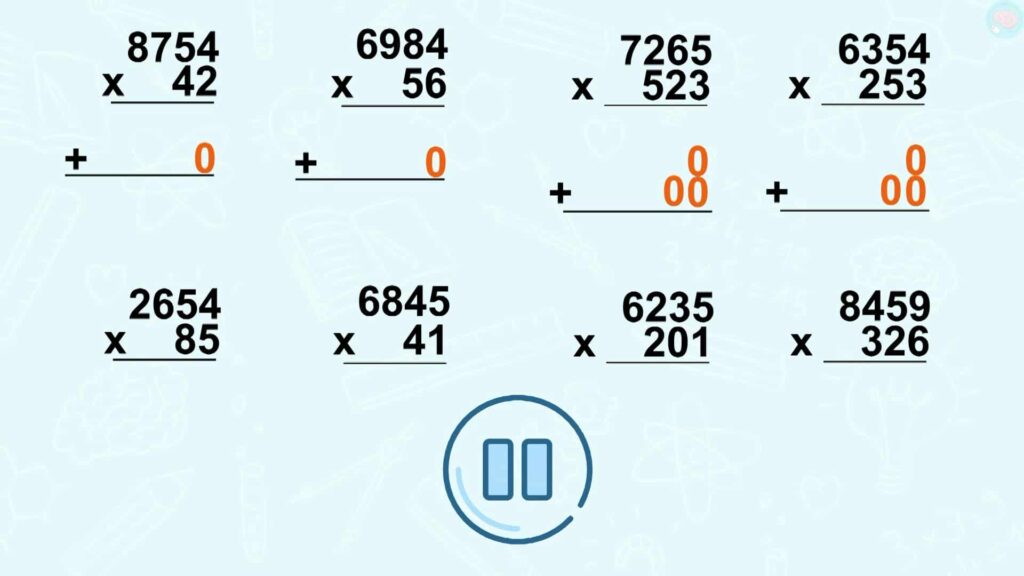
Est-ce que tu vas bien ? Est-ce que tu es toujours là, toi derrière ton écran ? C’est bien, car ce n’était pas facile et je suis allé vite pour faire les calculs. N’hésite pas à revoir la vidéo, même au ralenti. Comme toujours, pour que ton cerveau retienne bien les techniques, il faut s’entraîner, sinon il oublie. Pour cela, voici plusieurs multiplications posées que tu peux faire sur une feuille ou une ardoise. Pense à bien aligner les chiffres. Quand tu as fait les multiplications, pense à faire les additions comme je te l’ai montré ici. Dans les calculs suivants, je ne le montre plus. Tu peux mettre pause sur la vidéo pour réfléchir tranquillement et dans quelques secondes, je vais afficher les réponses.
Réponse
Voici les réponses, je ne vais pas détailler toutes les réponses, ça prendrait trop de temps. Mais à toi de bien comparer ce qui écrit sur ton écran et ce que tu as écrit sur ton ardoise ou ta feuille. Si tu as des erreurs, essaye de trouver d’où viennent ces erreurs, comme ça, les erreurs te permettent d’apprendre.

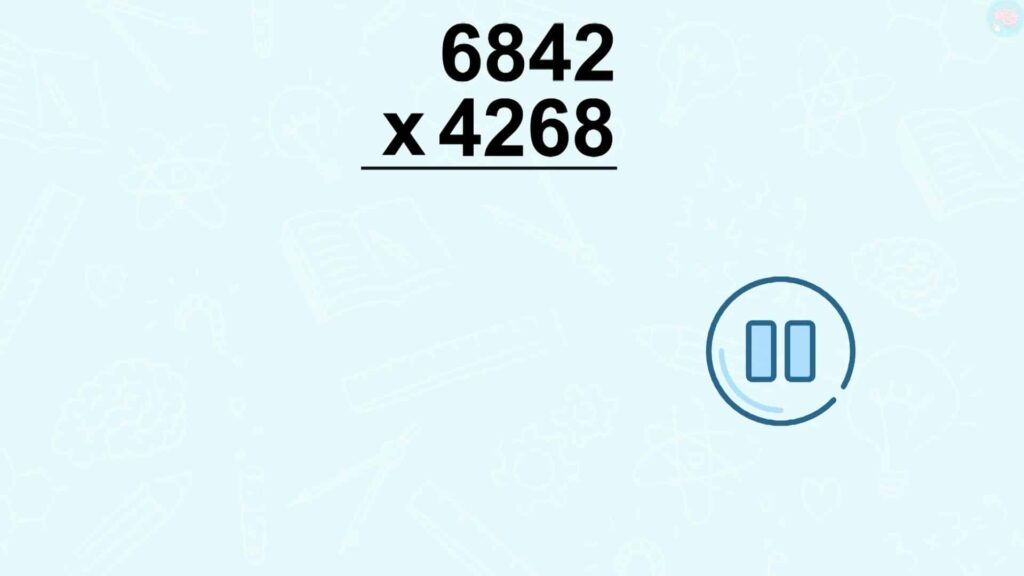
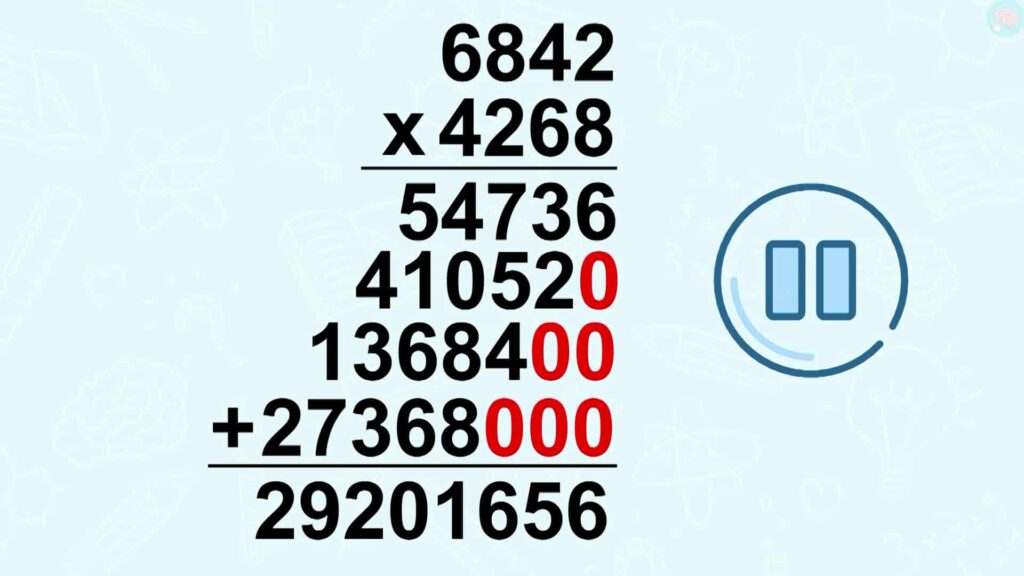
Si tu as envie en bonus, je te mets un calcul encore plus difficile avec quatre chiffres. La technique reste la même, mais fais bien attention aux 0 à ajouter. À toi, c’est parti.
Réponse
Et la réponse était, 29 2021 656.

Et c’est tout pour les multiplications à plusieurs chiffres, n’hésite pas à continuer à t’entraîner, car pour bien retenir la technique, il faut s’exercer. Pour cela, je t’ai préparé une fiche qui est sur le site maitrelucas.fr sous cette vidéo. Il y a aussi une carte mentale qui te permettra de revoir la leçon. À bientôt.




2 réponses sur « Les multiplications posées à plusieurs chiffres »
MERCI
tropp bienn