Il y a 7722 commentaires laissés par les utilisateurs sur le site. Laisser un commentaire pour cette vidéo
Leçons suggérées
Fiches exercices fractions à télécharger
Entraine-toi aux fractions grâce aux fiches que j’ai préparées :
DESCRIPTION
Comparer et calculer avec les fractions en CE1
Cette vidéo s’adresse aux élèves de CE1 (cycle 2) et dans celle-ci les élèves apprennent à comparer, additionner et soustraire des fractions. Je commence à leur rappeler ce qu’est une fraction en prenant l’exemple d’un gâteau. Si on le divise en plusieurs parts égales, chaque part est une fraction. Par exemple, si l’on divise un gâteau en quatre parts, chaque part est un quart.
Je leur montre aussi comment comparer des fractions, comme 3/10e et 2/10e, et pourquoi 3/10e est plus grand. Nous voyons ensemble que plus le numérateur (le nombre en haut de la fraction) est grand, plus la fraction est grande si le dénominateur (le nombre en bas) est le même.
Ensuite, je fais une comparaison entre 1/5 et 1/3, expliquant que plus le dénominateur est petit, plus la fraction est grande. Les élèves apprennent aussi à additionner des fractions comme 1/6e + 1/6e = 2/6e et à faire des soustractions simples avec des fractions.
Je termine la vidéo en proposant un petit problème pour bien comprendre ces notions.
LE CONSEIL DE MAITRE LUCAS
Les fractions sont partout au quotidien
Pour accompagner votre enfant dans l’apprentissage des fractions, l’idéal est de partir d’exemples concrets du quotidien. Par exemple, lorsque vous partagez un gâteau ou une pizza, c’est l’occasion parfaite pour lui montrer ce qu’est une fraction. Vous pouvez demander à votre enfant de diviser la nourriture en parts égales et d’exprimer cela sous forme de fractions. Cela permet de donner du sens aux concepts qu’il apprend à l’école.
L’important est d’encourager votre enfant à réfléchir en termes de comparaison. Si vous avez différents objets coupés en parts, vous pouvez lui demander quelle part est plus grande ou plus petite et pourquoi. En manipulant ces objets, il comprendra mieux la relation entre le numérateur et le dénominateur.
La pratique régulière est essentielle. Proposez à votre enfant des petits jeux à la maison où il peut additionner ou soustraire des fractions en s’amusant. Par exemple, si vous faites des activités créatives comme découper du papier, proposez-lui de colorier une fraction de la feuille et d’additionner les fractions colorées.
Compétences acquises
- Comprendre la notion de fraction.
- Savoir comparer des fractions de même dénominateur.
- Apprendre à additionner et soustraire des fractions simples.
À qui s’adresse cette vidéo ?
Niveau
CE1 (Cours élémentaires 1ère année)
Matière
Mathématiques, Maths
Cours
Fractions, nombres et calculs
Comparer et calculer avec des fractions
Tu as pris une plus grosse part de gâteau que moi, Papi.
— Mais non, j’ai pris 2/10 du gâteau, et toi tu as pris 3/10, donc tu en as plus que moi.
— Quoi, 3/10 c’est plus grand que 2/10 ?
— Maître Lucas !
— Oui.
— Papi dit que j’ai plus de gâteau que lui parce que j’ai 3/10 du gâteau et lui 2/10.
— C’est exact. Je te propose que, dans cette vidéo, nous apprenions à comparer des fractions et à faire des calculs avec les fractions.
Rappel Lire, écrire et représenter des fractions
Dans cette vidéo, nous avons déjà parlé de ce que sont les fractions.
Je te rappelle que si tu as un gâteau et que tu le partages en quatre parts égales, tu obtiens quatre quarts : un quart ici, un ici, un ici et un ici. Le quart s’écrit également comme cela : j’ai pris une part sur 4 en tout. Ce nombre, on l’appelle le numérateur, et celui-ci le dénominateur.
Si je prends cette bande de papier et que je la partage en 6, j’obtiens des sixièmes. La partie coloriée, c’est 1/6. Si j’en colorie 2, j’ai 2/6 ; 3, j’ai 3/6, etc. Toutes les parts du gâteau sont plus petites qu’un gâteau, donc toutes ces fractions sont plus petites que 1.
Comment comparer des fractions ?
Maintenant, revenons à vos parts de gâteau. Vous m’avez dit que vous aviez 2/10 et 3/10 du gâteau. Donc le gâteau est découpé en 10 parts égales.
Ton papi a deux parts de 1/10, et toi, tu as trois parts de 1/10 ; donc tu as une part de plus que lui, donc tu as plus de gâteau.
— Trop cool !
— De la même manière, 5/6 est plus grand que 4/6, puisque 5/6 c’est 5 parts, et 4/6 c’est 4 parts.
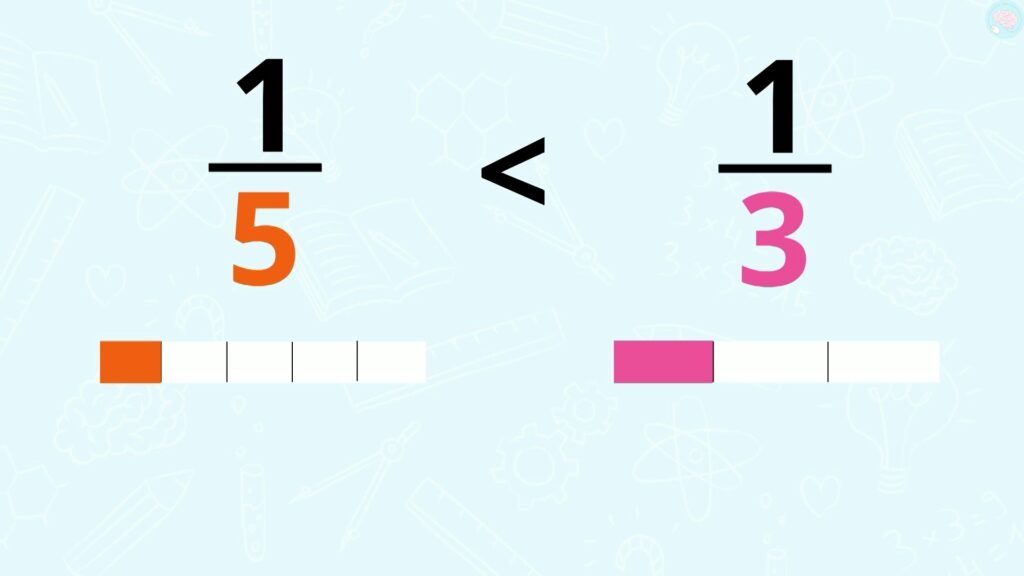
— J’ai compris ! Donc 1/5 est plus grand que 1/3 ?
— Ah non !
— Pourquoi non ?
— Je te montre. Je prends une bande de papier que je coupe en 5 : voici 1/5. Une autre que je coupe en trois : voici 1/3. Cette bande est partagée en 5 parts et celle-ci en trois, donc les parts de celle-ci sont plus petites que celle-là. Donc 1/5 est plus petit que 1/3.
Exercices sur comparer les fractions ?
Je sais que ce n’est pas toujours facile de comparer des fractions, alors je te propose de passer par des schémas.
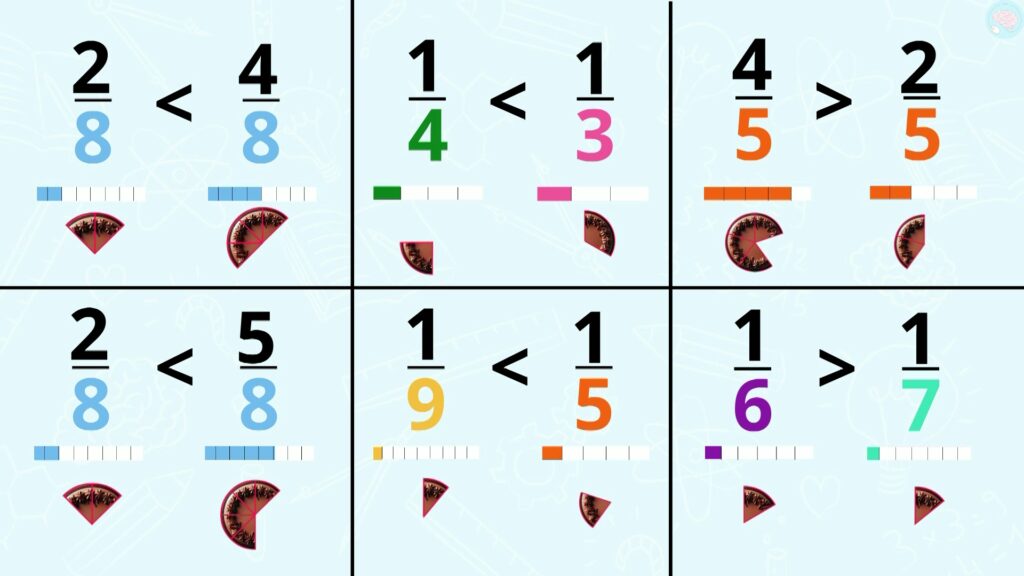
Regarde, voici plusieurs fractions avec, à chaque fois, un schéma. Je te propose de comparer les fractions. Par exemple, pour les premières, j’ai 2/8 ici et 4/8 là ; je vois que quatre parts, c’est plus que deux parts, donc 2/8 est plus petit que 4/8. Par contre, ici, j’ai 1/4 et ici 1/3 ; pour les deux fractions, je n’ai qu’une part, mais elles n’ont pas les mêmes tailles. Grâce à mon schéma, je vois que 1/4 est plus petit que 1/3. Fais la même chose pour les autres fractions en utilisant les signes « plus petit » ou « plus grand ». Tu fais ça sur une ardoise ou une feuille.
Réponse
Je commence par comparer 4/5 et 2/5. Ici, j’ai 4 parts sur 5 et ici 2 parts sur 5. J’ai donc plus de parts là : 4/5 est plus grand que 2/5. Ensuite, 2/8 et 5/8 ; ici, j’ai 2 parts sur 8 et ici 5 parts sur 8 ; 5/8, c’est plus grand que 2/8, donc 2/8 est plus petit que 5/8. Ensuite, 1/9 et 1/5 ; dans les deux cas, j’ai pris une part, mais ici, c’est une part sur 9 en tout, et ici une part sur 5 en tout. Donc une part sur 9 en tout, c’est forcément plus petit qu’une part sur 5, donc 1/9 est plus petit que 1/5. Ensuite, j’ai 1/6 et 1/7 ; dans les deux cas, j’ai pris une part, mais là, le gâteau est divisé par 6 et là par 7. Donc ici, les parts sont plus grandes puisqu’il y a moins de parts : 1/6 est plus grand que 1/7.
Additionner des fractions
Ensuite, je te montre comment faire quelques calculs avec des fractions. Prenons cette bande de papier que je divise en 6 ; je colorie une part, donc 1/6. Si je colorie deux parts, j’ai 2/6 ; donc ça veut dire que 1/6 + 1/6 = 2/6. Je continue : 3 parts, c’est 3/6, donc 1/6 + 1/6 + 1/6 = 3/6 ; 4 parts, c’est 4/6, donc 1/6 + 1/6 + 1/6 + 1/6 = 4/6, etc. Mais 6/6 alors ? Eh bien, 6/6, c’est le tout. 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6, c’est donc toute la bande : 6/6 = 1. De la même manière, 6/6 du gâteau, c’est un gâteau.
Soustraire des fractions
Et pour la soustraction, c’est la même chose : si j’ai 4/6 et que j’enlève 1/6, je vois sur mon schéma qu’il me reste 3/6, donc 4/6 – 1/6 = 3/6.
Exercices sur calculer les fractions
Passons tout de suite à la pratique. Toi, derrière ton écran, peux-tu faire ces quelques calculs ? Au départ, je t’ai mis des schémas à côté, et ensuite, tu essayes de les imaginer.
Réponse
Je passe à la correction. 1/4 + 3/4, je fais 1 + 3, ça fait 4, donc 4/4, et 4/4, c’est comme un gâteau entier, donc c’est égal à 1. 2/6 + 3/6, 2 + 3, 5, donc 5/6. 2/3 – 1/3, 2 – 1, 1, donc 1/3. 5/10 – 4/10, 1/10. 5/9 + 3/9, 8/9. 3/7 + 2/7, 5/7. 6/8 – 4/8, 2/8. Et 5/6 – 2/6 = 3/6. Tu peux comparer avec ce que tu as écrit, et si tu as des erreurs, refais les calculs ; comme ça, tes erreurs te permettent d’apprendre.
Et pour finir, je te propose un petit problème : voici une figure. Luna a colorié les 3/10 de cette figure en bleu ; quelle fraction de la figure est coloriée en rouge ? Dis-moi la réponse.
Réponse
Si je partage la figure en 10 parts égales, je vois qu’il y a 7/10 de la figure qui est coloriée en rouge. Je peux aussi faire une soustraction : 10/10, c’est toute la figure moins 3/10, pour ce qui est en rouge, ça fait 7/10.
Fiche exercices comparer er calculer les fractions
Dans cette vidéo, tu as appris à comparer des fractions, à en additionner et à en soustraire. Tu peux continuer à t’entraîner avec cette fiche d’exercices qui est sur le site maitrelucas.fr sous cette vidéo. Ce n’est pas le chapitre le plus facile à comprendre, alors ne te décourage pas si tu n’y arrives pas encore, et continues à t’entraîner. Tu verras que ça viendra. À bientôt !